Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications






Leçon 20: Le stacking: unir des modèles différents pour plus de performance
Toutes les leçons 

Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications
Leçon 14
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
Leçon 20
Le stacking: unir des modèles différents pour plus de performance
Le stacking: unir des modèles différents pour plus de performance
Le stacking: une autre pproche d’ensemble learning
Principe et mode de fonctionnement du stacking
Le stacking (stacked generalization) est une méthode d’ensemble learning qui vise à combiner plusieurs modèles différents afin d’améliorer la qualité des prédictions. Contrairement au bagging, qui repose sur la répétition d’un même type de modèle sur des sous‑échantillons, ou au boosting qui corrige les erreurs de manière séquentielle, le stacking cherche à exploiter la complémentarité entre des algorithmes hétérogènes.Dans le stacking, plusieurs modèles de base appelés learners de niveau 0 sont entraînés sur le même jeu de données et chacun produit ses propres prédictions. Ces prédictions sont ensuite utilisées comme nouvelles variables pour un modèle supplémentaire, appelé méta‑apprenant (ou learner de niveau 1). Ce méta‑modèle apprend à combiner les sorties des modèles de base afin de générer une prédiction finale plus robuste et plus précise.
Le stacking se distingue par sa logique d’agrégation. Là où le bagging mise sur la diversité des données et le boosting sur la pondération des erreurs, le stacking repose sur la diversité des algorithmes. En combinant des modèles de nature différente (par exemple un arbre de décision, une régression logistique et un SVM), il permet de capturer des aspects variés de la structure des données.
L'pproche basée sur le stacking présente plusieurs atouts. En effet, elle réduit le risque de surapprentissage lié à un modèle unique, elle exploite les forces de chaque algorithme et elle offre souvent des performances supérieures dans des contextes complexes. Le stacking est particulièrement utile lorsque les données présentent des relations non linéaires ou des patterns difficiles à saisir par un seul modèle.
Cependant, le stacking est plus coûteux en calcul puisqu’il nécessite l’entraînement de plusieurs modèles. Il peut aussi être sensible au surajustement si le méta‑apprenant est trop complexe. Enfin, il demande une bonne stratégie de validation croisée pour éviter les fuites d’information entre les niveaux d’apprentissage.
Nous aurons l'occasion de traiter en détail la technique de validation croisée plus loin dans ce cours.
Implémenter un modèle de stacking sur le dataset Titanic
Dans le code qui va suivre, la partie stacking consiste à entraîner en parallèle plusieurs modèles de base, à savoir, une régression logistique, un arbre de décision et un k‑NN, sur le jeu de données Titanic. Les prédictions qu’ils génèrent servent ensuite de nouvelles variables pour un modèle final, appelé méta‑apprenant (ici un Random Forest) qui sera chargé de combiner efficacement les sorties des modèles de base. Ce procédé exploite la complémentarité des algorithmes et permet d’obtenir une prédiction globale plus robuste et plus précise qu’avec un modèle unique.import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
import matplotlib.pyplot as plt
# Importation des modèles nécessaires
from sklearn.ensemble import StackingClassifier, RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
df = pd.read_csv("titanic.csv")
df = df[["Survived", "Pclass", "Sex", "Age", "SibSp", "Parch", "Fare"]].dropna()
df["Sex"] = df["Sex"].map({"male": 0, "female": 1})
X = df.drop("Survived", axis=1)
y = df["Survived"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Définition des modèles de base (level-0 learners)
base_learners = [
('lr', LogisticRegression(max_iter=1000, random_state=42)),
('dt', DecisionTreeClassifier(max_depth=5, random_state=42)),
('knn', KNeighborsClassifier(n_neighbors=5))
]
# Méta-apprenant (level-1 learner)
meta_learner = RandomForestClassifier(
n_estimators=100,
random_state=42,
n_jobs=-1
)
# Construction du StackingClassifier
clf = StackingClassifier(
estimators=base_learners,
final_estimator=meta_learner,
n_jobs=-1
)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Exactitude sur le jeu de test : {accuracy:.2f}")
cm = confusion_matrix(y_test, y_pred)
print(cm)
print(classification_report(y_test, y_pred))
Expliquons les parties importantes du code:
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, confusion_matrix, classification_report
import matplotlib.pyplot as plt
# Importation des modèles nécessaires
from sklearn.ensemble import StackingClassifier, RandomForestClassifier
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.neighbors import KNeighborsClassifier
df = pd.read_csv("titanic.csv")
df = df[["Survived", "Pclass", "Sex", "Age", "SibSp", "Parch", "Fare"]].dropna()
df["Sex"] = df["Sex"].map({"male": 0, "female": 1})
X = df.drop("Survived", axis=1)
y = df["Survived"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Définition des modèles de base (level-0 learners)
base_learners = [
('lr', LogisticRegression(max_iter=1000, random_state=42)),
('dt', DecisionTreeClassifier(max_depth=5, random_state=42)),
('knn', KNeighborsClassifier(n_neighbors=5))
]
# Méta-apprenant (level-1 learner)
meta_learner = RandomForestClassifier(
n_estimators=100,
random_state=42,
n_jobs=-1
)
# Construction du StackingClassifier
clf = StackingClassifier(
estimators=base_learners,
final_estimator=meta_learner,
n_jobs=-1
)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Exactitude sur le jeu de test : {accuracy:.2f}")
cm = confusion_matrix(y_test, y_pred)
print(cm)
print(classification_report(y_test, y_pred))
En plus du modèle Random Forest, cette instruction sert à importer la classe StackingClassifier qui est l’outil qui permet de mettre en place un stacking de la bibliothèque scikit-learn.
from sklearn.ensemble import StackingClassifier, RandomForestClassifier
Ensuite, on définit la liste des modèles de base (base_learners) utilisés dans le stacking:
base_learners = [
('lr', LogisticRegression(max_iter=1000, random_state=42)),
('dt', DecisionTreeClassifier(max_depth=5, random_state=42)),
('knn', KNeighborsClassifier(n_neighbors=5))
]
Dans ce code, la partie stacking définit trois modèles de base et qui sont une régression logistique, un arbre de décision et un k‑NN qui sont entraînés en parallèle sur le jeu de données Titanic. Ces trois modèles sont définits dans une liste python qu'on a identifiée par base_learners.
('lr', LogisticRegression(max_iter=1000, random_state=42)),
('dt', DecisionTreeClassifier(max_depth=5, random_state=42)),
('knn', KNeighborsClassifier(n_neighbors=5))
]
Dans ce code, la variable meta_learner correspond au modèle final du stacking, appelé méta‑apprenant:
meta_learner = RandomForestClassifier(
n_estimators=100,
random_state=42,
n_jobs=-1
)
n_estimators=100,
random_state=42,
n_jobs=-1
)
J'estime que vous connaissez désormais la significaiton des différents hyperparamètres du modèle Random Forest.
En fin, on définit le stacking à l'aide de ce code:
clf = StackingClassifier(
estimators=base_learners,
final_estimator=meta_learner,
n_jobs=-1
)
La variable clf instancie un objet StackingClassifier qui met en œuvre la logique du stacking. L'objet prend en entrée la liste des modèles de base définis dans base_learners (régression logistique, arbre de décision et k‑NN) et utilise comme modèle final meta_learner (ici un Random Forest) pour combiner leurs prédictions. L’argument n_jobs=-1 permet d’exploiter tous les cœurs du processeur afin d’accélérer l’entraînement. Ainsi, clf représente le classificateur complet basé sur le stacking, prêt à être entraîné et évalué sur les données du Titanic.
estimators=base_learners,
final_estimator=meta_learner,
n_jobs=-1
)
Après exécution, on obtient ce résultat:
Exactitude sur le jeu de test : 0.75
[[ 70 17 ]
[ 19 37 ]]
[[ 70 17 ]
[ 19 37 ]]
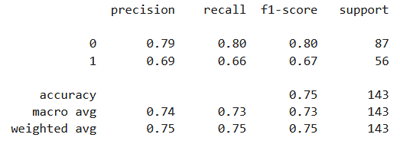
Les résultats obtenus peuvent sembler dans la norme, mais il est important de garder à l’esprit qu’ils dépendent fortement du choix des hyperparamètres. Je vous laisse donc le soin de les interpréter et les comparer avec ceux issus des autres modèles appliqués au même jeu de données afin d’évaluer si un ajustement des paramètres pourrait améliorer les performances.
Leçon 14
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
Leçon 20
Le stacking: unir des modèles différents pour plus de performance
Le stacking: unir des modèles différents pour plus de performance


