Classification supervisée par Naive Bayes

Rappel de la probabilité conditionnelle

L’algorithme Naive Bayes repose sur le principe fondamental de la probabilité conditionnelle qui permet d’estimer la probabilité qu’un événement se produise en tenant compte d’une information préalable. Formellement, la probabilité qu’une observation appartienne à une classe \(C\) sachant qu’elle possède certaines caractéristiques \(X\) s’écrit \(P(C\mid X)\).

Grâce au théorème de Bayes, cette probabilité peut être reformulée comme ceci:

• \(P(X\mid C)\): est la vraisemblance des données sous la classe \(C\).
• \(P(C)\): est la probabilité a priori de la classe.
• \(P(X)\): est la probabilité globale des données.

Exemple de diagnostic médical

Supposons qu’on cherche à estimer la probabilité qu’une personne soit malade (classe \(C=\mathrm{Malade}\)) sachant qu’elle présente un symptôme \(X=\mathrm{Fièvre}\).

La formule de Bayes nous dit:

• \(P(\mathrm{Malade}\mid \mathrm{Fièvre})\): Ce qu’on cherche, c'est à dire la probabilité d’être malade sachant qu’on a de la fièvre.
• \(P(\mathrm{Fièvre}\mid \mathrm{Malade})\): La probabilité qu’une personne malade ait de la fièvre (vraisemblance).
• \(P(\mathrm{Malade})\): La probabilité a priori d’être malade dans la population.
• \(P(\mathrm{Fièvre})\): La probabilité globale d’avoir de la fièvre (toutes causes confondues).

Expliquons ceci en chiffres en imaginant les données suivantes:

• \(P(\mathrm{Malade})=0,01\): 1% de la population est malade.
• \(P(\mathrm{Fièvre}\mid \mathrm{Malade})=0,9\): 90% des malades ont de la fièvre.
• \(P(\mathrm{Fièvre})=0,1\): 10% de la population a de la fièvre (malades ou non).

Alors:
Donc, même si la fièvre est fréquente chez les malades, la probabilité d’être malade sachant qu’on a de la fièvre n’est que de 9%, car la maladie est rare dans la population.

En résumé, le théorème de Bayes permet d’estimer la cause la plus probable à partir d’un effet observé en tenant compte du contexte global représenté par la probabilité a priori \(P(C)\) et la probabilité totale \(P(X)\). C’est précisément ce que fait l’algorithme Naive Bayes en classification. En effet, à partir des caractéristiques observées d’une instance, il calcule la probabilité d’appartenance à chaque classe et choisit celle qui est la plus vraisemblable.

Hypothèse dite "naïve"

Ce qui rend le modèle "naïf", c’est l’hypothèse forte selon laquelle toutes les variables explicatives (fièvre, toux, fatigue...) sont conditionnellement indépendantes entre elles, sachant la classe. Autrement dit, on suppose que la présence ou la valeur d’une caractéristique n’influence pas celle des autres, une hypothèse rarement vraie dans la réalité, mais qui fonctionne étonnamment bien dans de nombreux cas pratiques.

La formule simplifiée de \(P(X\mid C)\) dans le cadre de l’algorithme Naive Bayes repose sur l’hypothèse d’indépendance conditionnelle des variables explicatives \(x_1\),\(x_2\),...,\(x_n\) sachant la classe \(C\). Cette hypothèse permet de factoriser la probabilité conjointe en un produit de probabilités individuelles:
Autrement dit, au lieu d’estimer la probabilité conjointe complète (souvent complexe ou impossible à calculer directement), on suppose que chaque caractéristique \(x_i\) est statistiquement indépendante des autres une fois la classe \(C\) connue. Cela rend le calcul beaucoup plus simple et rapide tout en restant souvent performant en pratique.

Élaboration d’un modèle Naive Bayes pour la classification supervisée

Classification du dataset Iris avec Naive Bayes

Laissons les mathématiques de côté pour l’instant et concentrons-nous sur l’implémentation du modèle.

Nous allons reprendre le même jeu de données Iris que nous avons utilisé dans la leçon précédente avec la régression logistique. Ce dataset contient des mesures de fleurs appartenant à trois espèces différentes (Setosa, Versicolor et Virginica). L’objectif reste le même , c'est à dire, construire un modèle capable de prédire à quelle espèce appartient une fleur en fonction de ses caractéristiques. Cette fois-ci, nous allons aborder cette tâche avec une approche probabiliste en utilisant l’algorithme Naive Bayes.

Le code suivant importe les modules, charge le dataset et divise les données en train set et test set:
Vous avez certainement remarqué l'instruction d'importation du classifieur Naive Bayes gaussien depuis le module naive_bayes de la bibliothèque scikit-learn. Ce modèle est adapté aux données numériques continues supposées suivre une distribution normale (ou gaussienne), comme c’est le cas pour les variables du dataset Iris.
Maintenant, on charge le modèle, on l'entraine puis on procède aux prédictions sur le test set:
Evaluons les performances de notre modèle:
Suite à la première on instruction on obtient:

Accuracy: 0.9777777777777777

Quant à la fonction classification_report(), elle fournit des indicateurs détaillés pour chaque classe (Setosa, Versicolor, Virginica), à savoir la précision, le rappel, le F1-score et le support:
   
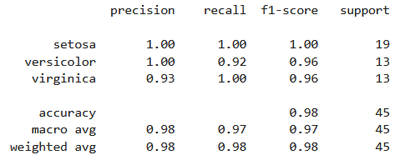
Le modèle atteint une précision globale (accuracy) de 97,8%, ce qui signifie qu’il a correctement classé 44 fleurs sur 45 dans l’ensemble de test. En effet, la classe Setosa a été parfaitement reconnue (précision, rappel et F1-score à 1.00). La classe Versicolor a enregistré une très bonne précision (1.00), mais un rappel de 0.92, ce qui indique qu’un petit nombre d’exemples de cette classe ont été mal classés. Enfin, la classe Virginica a montré un rappel parfait (1.00), mais une légère baisse de précision (0.93), ce qui signifie que quelques fleurs d’autres classes ont été attribuées à tort à Virginica.

En résumé, le modèle Naive Bayes fonctionne très bien sur ce jeu de données, avec une performance parfaite sur Setosa et des résultats très solides sur les deux autres classes.

Pour affiche la matrice de confusion (format texte), on exécute ce code:
Ce qui donne:
         
La matrice de confusion montre que le modèle Naive Bayes a correctement classé toutes les fleurs Setosa et Virginica, avec une seule erreur sur Versicolor, confondue une fois avec Virginica. Cela reflète une excellente performance globale, avec une très faible confusion entre les classes.          

Qu'est ce qui se passe au juste lors de l'entrainement d'un modèle Naive Bayes?

Modèle génératif vs modèle discriminatif

Naive Bayes est un modèle génératif qui apprend en comptant les fréquences. Lorsqu’on appelle model.fit(X, y), il ne cherche pas à optimiser une fonction coût, mais il se contente d’estimer les probabilités à partir des données. En effet, le modèle calcule la fréquence de chaque classe (comme "spam" ou "non spam") ainsi que la fréquence de chaque mot ou caractéristique dans chaque classe en supposant que les attributs sont indépendants les uns des autres. Ces statistiques suffisent pour appliquer le théorème de Bayes et prédire la classe la plus probable.

Contrairement à la régression logistique (qui est un modèle discriminatif qui apprend à séparer les classes en ajustant des coefficients pour chaque variable en minimisant une fonction coût grâce à un algorithme d’optimisation), Naive Bayes ne fait aucun ajustement de paramètres via descente de gradient ou autre algorithme d’optimisation. Il ne cherche pas à tracer une frontière entre les classes, mais à modéliser directement comment les données sont générées dans chaque classe. C’est ce qui le rend rapide, simple, mais parfois moins précis quand les variables sont corrélées.