Prédire des classes avec la régression logistique

Algorithmes de classification - Rappel

Dans la leçon consacrée à la classification supervisée, nous avons vu cette classe d'algorithmes de Machine Learning constitue une composante essentielle de l’apprentissage supervisé. Elle a pour objectif de prédire une variable cible qualitative (également appelée variable catégorielle) à partir d’un ensemble de variables explicatives. Contrairement à la régression, qui cherche à estimer une valeur continue, la classification vise à associer chaque observation à l’une des classes définies au préalable.

L’un des algorithmes les plus emblématiques de la classification supervisée est la régression logistique, d'autant plus qu'il est compté parmi les plus accessibles sur le plan conceptuel.

Régression logistique: mode de fonctionnement

La régression logistique est un algorithme de classification supervisée utilisé pour prédire une variable catégorielle qui est souvent binaire (par exemple: oui/non, spam/non spam, malade/sain...).

Contrairement à la régression linéaire qui estime une valeur continue, la régression logistique cherche à modéliser la probabilité qu’une observation appartienne à une classe donnée. Elle repose sur une fonction mathématique appelée sigmoïde, qui transforme une combinaison linéaire des variables explicatives en une probabilité comprise entre 0 et 1.

Le cœur du modèle de régression logistique est une équation linéaire des variables indépendantes similaire à celle de la régression linéaire:
Cette valeur z est ensuite passée dans la fonction sigmoïde:
Le résultat \(p\) représente la probabilité que l’observation appartienne à la classe positive. En fixant un seuil de décision (souvent 0.5), on peut convertir cette probabilité en prédiction catégorielle. Par exemple:

• Si \(p\geq 0.5\), on prédit la classe 1.
• Si \(p<0.5\), on prédit la classe 0.

La régression logistique est appréciée pour sa simplicité, sa rapidité et sa capacité d’interprétation. En effet, chaque coefficient \(\beta _i\) indique l’impact d’une variable sur la probabilité d’appartenance à une classe. Elle fonctionne bien lorsque les classes sont linéairement séparables. Par contre, elle peut être limitée en présence de relations complexes ou non linéaires.

La régression logistique constitue souvent une porte d’entrée idéale dans le monde de la classification, avant d’aborder des modèles plus sophistiqués comme les arbres de décision ou les SVM (qu'on aura l'occasion de voir dans la suite de ce cours).

Données linéairement séparables: définition et implications

On dit que des données sont linéairement séparables lorsqu’il est possible de tracer une ligne droite (en 2D), un plan (en 3D) ou un hyperplan (en dimensions supérieures) qui sépare parfaitement les classes sans ambiguïté. Autrement dit, il existe une frontière linéaire qui divise l’espace des données en deux zones distinctes, chacune contenant uniquement les points d’une seule classe.

Ce concept est fondamental car certains algorithmes (comme la régression logistique, le SVM linéaire ou la perceptron simple) reposent sur l’hypothèse que les classes peuvent être séparées par une frontière linéaire. Si les données ne sont pas linéairement séparables (par exemple, si les classes sont entremêlées ou forment des cercles), ces modèles auront du mal à bien classifier. Dans ce cas, on peut soit transformer les données à l'aide du feature engineering, soit utiliser des modèles plus flexibles comme les arbres de décision ou les réseaux de neurones.

Extension de la régression logistique aux problèmes multiclasses

Bien que la régression logistique soit historiquement conçue pour des problèmes de classification binaire, elle peut être étendue aux cas multiclasses grâce à plusieurs stratégies. Cette généralisation permet de traiter des situations où la variable cible comporte plus de deux catégories. Les principales variantes sont :

• One-vs-Rest (OvR): On entraîne un modèle binaire pour chaque classe en la comparant aux autres. Lors de la prédiction, on choisit la classe dont le modèle donne la probabilité la plus élevée.
• Softmax (régression logistique multinomiale): une approche plus intégrée qui calcule directement les probabilités pour chaque classe via une fonction de normalisation exponentielle.
• One-vs-One (OvO): on construit un modèle pour chaque paire de classes, puis on utilise un vote majoritaire pour la prédiction finale.

Ces variantes permettent à la régression logistique de rester un outil performant et interprétable, même dans des contextes à plusieurs classes.
   

Application de la régression logistique au dataset Iris

Présentation du dataset Iris (Iris de Fisher)

Un exemple classique pour illustrer la classification multiclasses est le jeu de données Iris, proposé par le statisticien Ronald Fisher. D'ailleurs ce dataset est aussi connu sous le nom d'Iris de Fisher. Ce dataset contient 150 observations de fleurs appartenant à trois espèces: Iris setosa, Iris versicolor et Iris virginica. Chaque fleur est décrite par quatre caractéristiques mesurées en centimètres : la longueur et la largeur des pétales, ainsi que la longueur et la largeur des sépales. Ce jeu de données (accessible directement depuis scikit-learn) est particulièrement apprécié pour sa simplicité, sa structure équilibrée et sa visualisation intuitive, ce qui en fait un excellent point de départ pour expérimenter la régression logistique en mode multiclasses.

Construction, entrainement et évaluation du modèle de régression logistique

Le pipeline d’élaboration d’un modèle de régression logistique suit une structure très proche de celle de la régression linéaire que nous avons déjà rencontrée à plusieurs reprises. On retrouve les mêmes étapes qui consistent à la préparation des données, la séparation en ensembles d’entraînement et de test, l'entraînement puis évaluation du modèle.

La principale différence réside dans la nature discrète de la variable cible, qui représente une classe plutôt qu’une valeur continue. Par conséquent, les métriques d’évaluation changent également. En effet, on privilégie des indicateurs comme l'exactitude (accuracy), la précision, le rappel (recall), le score F1 ou encore la matrice de confusion, plutôt que l’erreur quadratique moyenne ou le coefficient de détermination R².

Commençons par importer les modules requis:
Le dataset Iris, le modèle LogisticRegression et la fonction train_test_split ont été importés à partir de sckit-learn. Ensuite nous avons importé les métriques optimisés pour les problèmes de classification, à savoir:

• classification_report: qui calcule les métriques Precision, Recall et F1-Score qu'on a déjà vu dans leçon consacrée à la classification supervisée
• confusion_matrix: (ou matrice de confusion) est un graphique qui permet de visualiser les erreurs de prédiction en comparant les classes prédites par le modèle aux classes réelles.
• accuracy_score: qui indique la proportion globale de prédictions correctes.

En plus de matplotlib, nous avons aussi importé la bibliothèque seaborn qui permet de générer des graphiques plus esthétique et plus rapide à configurer. On en aura besoin pour traçer la matrice de confusion.

La prochaine étape consiste à importer les données:
L'objet X est une matrice NumPy de forme (150, 4), où chaque ligne représente une fleur, et chaque colonne une caractéristique mesurée. Ces caratéristiques sont "Longueur sépale", "Largeur sépale", "Longueur pétale","Largeur pétale".

L'objet y est un vecteur NumPy de longueur 150, contenant les étiquettes de classe pour chaque fleur, et qui sont: 0 (Iris setosa), 1 (Iris versicolor) et 2 (Iris virginica).

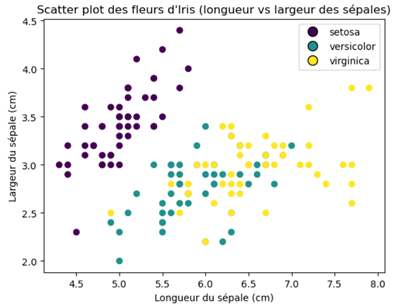
Essayons de tracer un graphique qui illustre la distribution des espèces d'Iris selon la longueur et la largeur du sépale:
Je pense que vous avis compris ce bout de code vu qu'on l'exécute souvent (à quelques différences près).

Les valeurs X[:,0], X[:,1] désignent toutes les lignes de la première et la deuxième colonne du dataset. C'est à dire, toutes les longueurs et largeurs de sépale disponibles (150 en tout). Quant à c=y, elle désigne que la couleur n’est pas définie manuellement (comme 'red' ou '#FF0000'), mais automatiquement dérivée des valeurs de y. C'est à dire que les valeurs de y (0, 1 et 2) sont interprétées comme des indices de classe et associe automatiquement 3 couleurs distinctes.

Après exécution, on obtient l'illustration suivante:
         
La prochaine étape consiste à séparer les données d'entrainement de celles de l'évaluation, l'entrainement du modèle et la génératin des prédictions à partir des données de test:

L'argument max_iter=200 est le nombre maximal d’itérations que l’algorithme d’optimisation est autorisé à effectuer pour converger vers une solution stable.

Evaluation du modèle

Nous arrivons à l’étape d’évaluation du modèle de classification. Pour cela, nous allons mobiliser un ensemble de métriques spécifiquement conçues pour ce type de tâche.

Commençons par la métrique Accuracy (ou exéctitude):
Cela donne:
Une exéctitude de 1.00 signifie que notre modèle a prédit correctement toutes les classes sur l’ensemble de test. En d’autres termes, 100% des prédictions sont exactes.

Un score d’accuracy de 1.00 peut sembler idéal, mais il ne garantit pas à lui seul la qualité du modèle. Sur des jeux de données très petits ou bien structurés comme Iris, une telle performance est plausible. En revanche, dans des contextes plus complexes ou déséquilibrés, l’accuracy peut être trompeuse.

Par exemple, si un jeu de données contient 95% d’échantillons de la classe 1 et seulement 5% de la classe 2, un modèle qui prédit systématiquement la classe 1 obtiendra une accuracy de 95%. Ce score peut sembler excellent à première vue, mais il est en réalité trompeur, car le modèle échoue totalement à reconnaître la classe minoritaire. C'est pour cette raison qu'il est crucial d'évaluer le modèle à travers d'autres métriques comme la précision, le rappel et le score F1.

Exécutons ce code:
Cette portion de code affiche un rapport de classification détaillé pour notre modèle en utilisant la fonction classification_report de scikit-learn comme l'illustre cette figure:

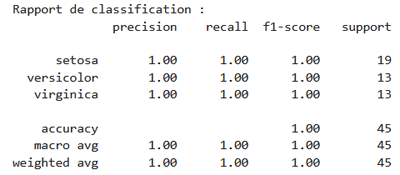
Le résultat affiché est un tableau de métriques pour chaque classe (setosa, versicolor, virginica), basé sur:

• Précision (precision): proportion de vraies prédictions positives parmi toutes les prédictions positives.
• Rappel (recall): proportion de vraies prédictions positives parmi toutes les vraies instances positives.
• Score F1 (f1-score): moyenne harmonique entre précision et rappel.
• Support: nombre d’échantillons réels dans chaque classe.

En somme, le rapport de classification indique une performance parfaite du modèle. En effet, toutes les fleurs ont été correctement classées dans leurs catégories respectives (setosa, versicolor et virginica), avec une précision, un rappel et un score F1 de 1.00 pour chaque classe. L’accuracy globale est également de 100%, ce qui signifie que le modèle n’a commis aucune erreur sur les 45 échantillons testés. Les moyennes macro et pondérée confirment cette homogénéité dans la qualité des prédictions.

Matrice de confusion (confusion matrix)

La matrice de confusion permet d’évaluer finement les performances d’un modèle de classification en comparant les prédictions aux valeurs réelles.

Chaque ligne de la matrice de confusion représente une classe réelle et chaque colonne une classe prédite. Les valeurs sur la diagonale indiquent les bonnes prédictions, tandis que les cases hors diagonale révèlent les erreurs de classification. Elle aide ainsi à identifier quelles classes sont correctement reconnues et lesquelles sont confondues, offrant une lecture plus nuancée que l’accuracy seule.

La matrice de confusion peut être générée de deux façons: soit affichée sous forme de tableau textuel, soit représentée visuellement à l’aide d’un graphique pour une lecture plus intuitive.

Pour avoir un tableau textuel on exécute ce code:
On obtient:
Pour générer la matrice de confusion sous forme de graphique, on exécute ce bloc d'instructions:
Ce qui produit cette figure:


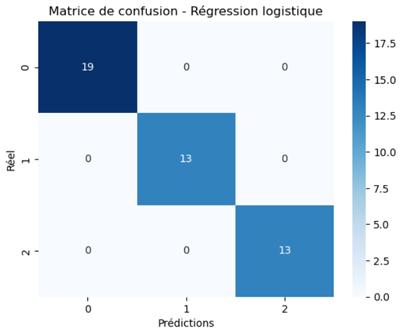
Dans cette instruction:
on a utilisé Seaborn pour afficher une matrice de confusion sous forme de carte thermique (heatmap).

Voici une explication rapide des arguments qu'on a passé à la méthode heatmap:

• cm: la matrice de confusion obtenue via confusion_matrix(y_test, y_pred).
• annot=True: affiche les valeurs numériques dans chaque case de la matrice.
• cmap='Blues': applique une palette de couleurs bleue pour visualiser l’intensité (plus la case est foncée, plus la valeur est élevée).

Quant aux autres instructions du bloc, elles ont déjà été abordées à plusieurs reprises dans les leçons précédentes.

En observant la matrice de confusion, on constate immédiatement que le modèle a parfaitement reconnu chaque classe. En effet, toutes les prédictions se trouvent sur la diagonale, ce qui indique une classification exacte, tandis que les cases hors diagonale sont nulles, ce qui révèle l’absence totale d’erreurs.