Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications






Leçon 7: Comment un modèle de Machine Learning apprend-il?
Toutes les leçons 

Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications
Leçon 7
Comment un modèle de Machine Learning apprend-il?
Comment un modèle de Machine Learning apprend-il?
Démarche d'apprentissage d'un modèle de régression linéaire
Objectif de cette leçon
Cette leçon a pour but de vous faire comprendre comment un modèle peut apprendre à partir de données étiquetées dans le cadre de l’apprentissage supervisé. Pour cela, nous allons partir d’un exemple simple et concret. Il s'agit d'un modèle de régression linéaire avec une seule variable d’entrée. Ce choix nous permettra de démystifier les mécanismes fondamentaux de l’apprentissage automatique, sans complexité inutile.Nous allons voir notamment:
- Ce qu’est une fonction coût (et pourquoi elle est essentielle)
- Comment un modèle ajuste ses paramètres pour réduire l’erreur
- Et le rôle de la descente du gradient dans ce processus d’optimisation
À retenir: Même si l’exemple est simplifié, les principes que nous allons voir ici s’appliquent à la grande majorité des modèles que nous verrons par la suite. Dans les prochaines leçons, nous explorerons différents algorithmes, leurs logiques de fonctionnement et des exemples de code pour les mettre en pratique (sans entrer dans les détails mathématiques avancés). L’objectif est de vous donner une intuition solide et des références concrètes pour comprendre comment les modèles apprennent.
Mise en situation: prédire le prix d’un fruit selon son poids
Imaginons que nous souhaitons prédire le prix d’un fruit en fonction de son poids. Prenons l’exemple des pastèques.Nous disposons du jeu de données suivant :
| Poids (x) | Prix (y) |
| 1 | 2 |
| 2 | 4 |
| 3 | 6 |
| 4 | 8 |
Nous faisons l’hypothèse que le prix peut être estimé par une relation linéaire simple :
\(\hat {y}=\theta \cdot x\)
Où \(x\) est le poids du fruit, et \(\theta\) est le paramètre que le modèle doit apprendre.
L’objectif du modèle est de déterminer la valeur optimale de son paramètre θ pour que la courbe qu’il trace corresponde au mieux aux données observées. Le graphique ci-dessous illustre cette progression. En effet, les points représentent le poids et le prix de pastèques, tandis que les différentes courbes montrent les étapes successives d’ajustement du modèle. La première ligne (choisie arbitrairement) s’éloigne des données, mais les suivantes s’en rapprochent progressivement. La courbe finale épouse parfaitement la tendance en traduisant l’amélioration du modèle au fil des ajustements. Ce visuel rend tangible le processus par lequel un modèle affine ses prédictions pour mieux refléter la réalité.
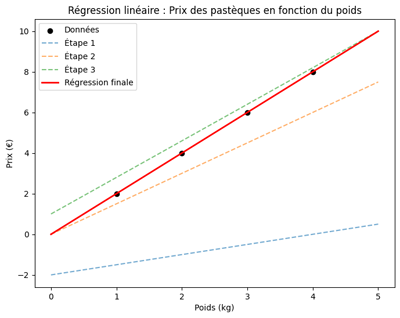
Dans cet exemple, les données suivent une linéarité parfaite, ce qui est rare (voire inexistant) dans les cas réels. En pratique, même lorsque les données présentent une tendance linéaire, les points s’écartent généralement de la droite de régression. Nous explorerons des exemples concrets dans les prochaines leçons.
Voyons maintenant comment le modèle arrive-t-il à améliorer le paramètre θ.
Fonction coût (loss function) pour mesurer l’erreur
La fonction coût (appelée aussi loss function) est un outil mathématique qui permet d’évaluer la performance d’un modèle de Machine Learning. Elle mesure l’écart entre les prédictions du modèle et les valeurs réelles observées dans les données. Plus cet écart est grand, plus la fonction coût est élevée, ce qui indique que le modèle est mal ajusté. Dans notre exemple où le prix des pastèques dépend du poids, la fonction coût peut être exprimée par la formule suivante :\(J(\theta )=\frac{1}{m}\sum _{i=1}^m\left( \hat {y}_i-y_i\right) ^2\)
- \(\hat {y}_i\): Prix prédit par le modèle pour le poids \(x_i\)
- \(y_i\): Prix réel (qui figure dans le dataset)
- \(m\): Nombre d’exemples
- \(\theta\): Paramètre du modèle (que l'on cherche à optimiser)
Cette formule correspond à l’erreur quadratique moyenne, couramment utilisée pour les modèles de régression. Sa représentation graphique ressemble à ceci:
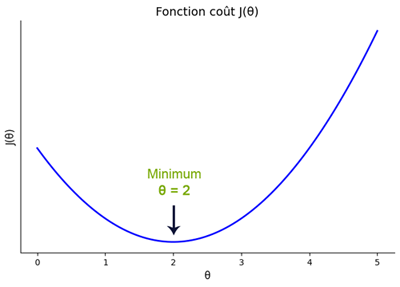
Cette illustration représente la fonction coût \(J(\theta )\) qui évalue la qualité des prédictions du modèle en fonction du paramètre \(\theta \) . La courbe en forme de parabole montre que certaines valeurs de \(\theta \) donnent de mauvaises prédictions (coût élevé), tandis qu’une valeur bien précise minimise cette erreur. Contrairement à l’illustration précédente (où l’on visualisait l’ajustement progressif de la courbe de régression aux points du dataset) cette figure permet de comprendre comment le modèle "sait" qu’il progresse, en cherchant à descendre vers le bas de cette courbe. Donc, chaque position sur cette parabole donne lieu à une courbe de régression différente et le point le plus bas engendre la courbe idéale ajustée aux données du dataset.
Optimisation du modèle: descente du gradient
En apprentissage automatique, le but principal consiste à optimiser un modèle, c’est-à-dire minimiser une fonction coût (loss function) qui mesure l’erreur entre les prédictions du modèle et les résultats attendus.Pour notre modèle \(\hat {y}=\theta x\), on a utilisé la fonction de coût quadratique qui calcule l’erreur moyenne entre les prédictions \(\hat {y}_i\) et les vraies valeurs \(y_i\):
\(J(\theta ) = \frac{1}{m}\sum _{i=1}^m\left( \hat {y}_i-y_i\right) ^2 = \frac{1}{m}\sum _{i=1}^m(\theta x_i-y_i)^2\)
La descente du gradient (ou gradient descent) est une méthode qui permet de trouver la meilleure valeur de \(\theta\) en suivant la pente de cette fonction.
On commence par calculer le gradient, c’est-à-dire la dérivée de \(J(\theta )\), donnée par:
\(\nabla _{\theta }J(\theta ) = \frac{\partial J}{\partial \theta }=\frac{2}{m}\sum _{i=1}^m(\theta x_i-y_i)\cdot x_i\)
Ensuite, on ajuste \(\theta\) dans le sens opposé à cette pente:
\(\theta :=\theta -\alpha \cdot \nabla _{\theta }J(\theta )\)
Où \(\alpha\) est un petit nombre appelé taux d’apprentissage (ou learning rate). Ce processus est répété jusqu’à ce que l’erreur soit minimale. Ce qui permet au modèle d’apprendre progressivement à faire de bonnes prédictions.
Le coefficient \(\alpha\) est appelé hyperparamètre. Il n’est pas appris par le modèle mais choisi à l’avance pour contrôler la vitesse de convergence. Si \(\alpha\) est trop grand, le modèle risque de diverger, c'est à dire de dépasser le point le plus bas de la fonction coût sans jamais l'atteindre. S’il est trop petit, l’apprentissage sera très lent. Donc, le choix d'une bonne valeur pour cet hyperparamètre est capital.
À la fin du processus d’apprentissage, le modèle parvient à déterminer une valeur optimale de \(\theta\) qui lui permet de tracer une courbe de régression bien ajustée aux données d’entraînement (comme illustré sur la figure ci-dessous).
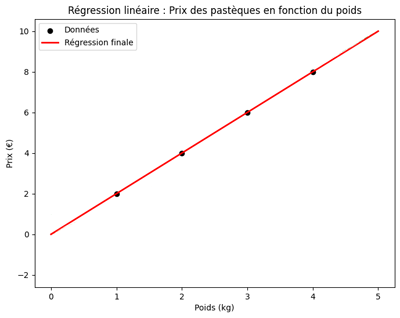
Grâce à cet ajustement, il devient capable de généraliser et de faire des prédictions fiables sur de nouvelles données qu’il n’a jamais rencontrées auparavant.
Dans notre exemple, le modèle a déterminé que la valeur optimale de \(\theta\) est égale à 2. Cela signifie que pour estimer le prix d’une pastèque, il suffit de multiplier son poids par deux.
Et si le modèle doit ajuster plusieurs paramètres?
Dans les problèmes de régression plus réalistes, le modèle ne se limite généralement pas à une seule variable d’entrée. En effet, il utilise plusieurs features (variables explicatives) pour mieux capturer la complexité des données et il intègre très souvent un biais (ou intercept) pour permettre un décalage vertical de la courbe de prédiction.L’ensemble de ces éléments (les coefficients associés à chaque feature et le biais) constitue les paramètres du modèle qu’il faut ajuster automatiquement pour minimiser l’erreur entre les prédictions et les valeurs réelles. Pour cela, on applique exactement le même principe que dans le cas simple vu précédemment. Donc, on définit une fonction de coût, on calcule son gradient puis on met à jour les paramètres par descente du gradient.
Cependant, la seule différence est que, pour gérer efficacement plusieurs variables et exemples, on représente les données sous forme de matrices et vecteurs. Cela permet d’effectuer les calculs de manière plus rapide, plus compacte et adaptée aux grandes dimensions. Cette approche matricielle est au cœur de l’optimisation dans les modèles de régression linéaire multivariée et aussi d'autres types de modèles de Machine Learning et du Deep Learning.
L’importance de maîtriser les bases avant d’utiliser les bibliothèques
Cette leçon avait pour objectif de vous faire comprendre le fonctionnement général de l’apprentissage d’un modèle à travers un exemple simple et accessible. Dans la suite de ce cours, toutes ces étapes seront prises en charge automatiquement par des bibliothèques spécialisées qui utilisent des opérations matricielles pour accélérer et optimiser les calculs.Toutefois, connaître ce qui se passe "sous le capot" reste essentiel pour bien comprendre les mécanismes d’apprentissage et interpréter les résultats de manière éclairée.
Leçon 7
Comment un modèle de Machine Learning apprend-il?
Comment un modèle de Machine Learning apprend-il?


