Régression et classification dans l'apprentissage supervisé

Rappel de l'apprentissage supervisé

Comme on l'a vu dans la leçon consacrée aux types d'apprentissages, l’apprentissage supervisé est une branche du Machine Learning où l’on dispose d’un ensemble de données annotées (ou étiquetées). Chaque exemple dans le dataset est associé à une sortie attendue appelée "label". L’objectif est d’apprendre au modèle de produire une fonction qui relie les entrées X aux sorties y afin de pouvoir prédire la sortie pour de nouvelles données. C’est le paradigme le plus utilisé en pratique, notamment pour des tâches comme la prédiction de prix, la détection de fraude ou la reconnaissance d’images.

Les deux volets de l'apprentissage supervisé: régression et classification

L’apprentissage supervisé regroupe deux grandes catégories de tâches, à savoir la régression et la classification. Dans les deux cas, le modèle apprend à prédire une sortie à partir d’exemples annotés, mais la nature de cette sortie diffère.

En régression, il s’agit de prédire une valeur continue, comme le prix d’un logement, la température d’un jour donné, le revenu annuel d’un individu ou encore la durée d’un trajet. Ces prédictions peuvent prendre n’importe quelle valeur numérique dans un intervalle donné.

À l’inverse, la classification consiste à prédire une catégorie discrète, comme le type d’un animal (chat, chien, oiseau), le genre d’un film (comédie, drame, action) ou le statut d’un email (spam ou non spam). Certaines tâches peuvent même impliquer plusieurs classes, comme la reconnaissance de chiffres manuscrits (0 à 9) ou la détection de pathologies médicales parmi plusieurs diagnostics possibles.

Cette distinction fondamentale influence le choix des algorithmes, des métriques d’évaluation et des cas d’usage. Par exemple, prédire le score d’un étudiant à un examen relève de la régression, tandis que déterminer s’il réussira ou échouera relève de la classification. Comprendre cette dualité est essentiel pour aborder la modélisation avec clarté et pertinence.

La régression: prédire une valeur continue

Qu'est ce que la régression?

La régression est une approche de l’apprentissage supervisé utilisée lorsque la variable dépendante (ou cible) est quantitative continue, c’est-à-dire qu’elle peut prendre une infinité de valeurs numériques sur un intervalle donné. Elle vise à modéliser la relation entre cette variable cible et une ou plusieurs variables indépendantes (ou explicatives), qui peuvent être quantitatives ou qualitatives. Par exemple, prédire le prix d’un logement à partir de sa surface, sa localisation et son nombre de pièces, est une tâche de régression. De même, estimer la température d’un jour donné en fonction de l’humidité et de la pression atmosphérique, ou anticiper le score d’un élève selon ses heures d’étude et ses résultats précédents, relèvent de cette catégorie.

Cette illustration représente un nuage de points bleus (les observations réelles qui figurent dans le dataset) avec une courbe de régression orange (calculée par le modèle):

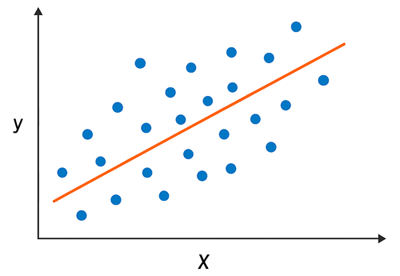
Les modèles de régression cherchent à minimiser l’écart entre les valeurs prédites par le modèle et les valeurs réelles observées dans le jeu de données. Cet écart est souvent mesuré par des fonctions de coût (loss function) comme l’erreur quadratique moyenne (MSE) ou l’erreur absolue moyenne (MAE), qui permettent d’évaluer la qualité des prédictions.

Algorithmes populaires de régression

Il existe un grand nombre d'algorithmes de régression, parfois même certains algorithmes connus pour les tâches de classification peuvent aussi être utilisées dans des problèmes de régression. Les algorithmes les plus connus sont:

• Régression linéaire simple et multiple: Il s'agit de l'algorithme de base qui cherche une relation linéaire entre les variables indépendantes et la variable cible. Il est facile à interpréter, mais limité aux relations linéaires.
• Régression Ridge (L2): Cet algorithme ajoute une pénalisation sur les coefficients pour éviter le sur-apprentissage (overfitting). Il est utile quand les variables sont corrélées.
• Régression Lasso (L1): Il est similaire à la régression Ridge, mais peut annuler certains coefficients, ce qui permet une sélection automatique de variables (réduction de dimensions).
• Support Vector Regression (SVR): Il s'agit d'une extension de l'algorithme SVM utilisé en classification mais adapté aux problèmes de régression. Il utilise des marges et des noyaux pour modéliser des relations non linéaires.

On peut également trouver des algorithmes de régression à base d'arbres, ensemblistes, probabilistes ou à base de distances.

Estimer les performances d'un modèle de régression: Les métriques

Une métrique est une fonction ou un indicateur quantitatif utilisé pour évaluer la performance d’un modèle d’apprentissage automatique. Elle permet de mesurer l’écart entre les prédictions du modèle et les valeurs réelles (représentées par les labels présents dans le dataset), selon des critères adaptés à la nature de la tâche (régression, classification...).

En pratique, une métrique traduit en un score numérique la qualité des prédictions, facilitant ainsi la comparaison entre plusieurs modèles ou configurations.

Les métriques les plus utilisées en Régression sont:

MAE: Mean Absolute Error
L’erreur absolue moyenne (MAE) est une mesure simple qui calcule l’écart moyen entre les valeurs prédites par le modèle et les valeurs réelles observées en prenant la valeur absolue de chaque différence. Elle s’exprime dans les mêmes unités que la variable cible, ce qui la rend facilement interprétable. Par exemple, si l’on prédit des prix immobiliers, une MAE de 5000 signifie que le modèle se trompe en moyenne de 5000 unités monétaires. Cette métrique est robuste face aux valeurs aberrantes modérées, mais elle ne pénalise pas fortement les grandes erreurs.

MSE: Mean Squared Error
L’erreur quadratique moyenne (MSE) est une métrique qui calcule la moyenne des carrés des écarts entre les prédictions et les valeurs réelles. En élevant les erreurs au carré, elle accorde un poids plus important aux écarts importants, ce qui permet de détecter les modèles qui commettent des erreurs majeures. Toutefois, cette sensibilité aux valeurs extrêmes peut être un inconvénient dans certains contextes. De plus, la MSE s’exprime dans des unités au carré (par exemple: euros²), ce qui la rend moins intuitive à interpréter directement.

RMSE: Root Mean Squared Error
La racine de l’erreur quadratique moyenne (RMSE) est simplement la racine carrée de la MSE. Elle combine les avantages de la MSE (pénalisation des grandes erreurs) avec une meilleure lisibilité, puisqu’elle revient dans les mêmes unités que la variable cible. Une RMSE de 7 signifie que les prédictions s’écartent en moyenne de 7 unités de la réalité, en tenant compte de la gravité des erreurs. Si la RMSE est nettement plus élevée que la MAE, cela peut indiquer la présence d’erreurs importantes ou de valeurs aberrantes dans les prédictions.

R2: R squared score
Le R squared score (ou coefficient de détermination R2) mesure la proportion de la variance de la variable cible qui est expliquée par le modèle. Il varie généralement entre 0 et 1, bien qu’il puisse être négatif si le modèle est moins performant qu’une prédiction constante. Un R2 de 0.85 indique que 85% de la variabilité des données est captée par le modèle. Cette métrique donne une vision globale de la qualité du modèle, mais elle peut être trompeuse si utilisée seule, notamment en présence de données non linéaires ou de sur-ajustement. Il existe aussi une version ajustée du R2, utile pour comparer des modèles avec des nombres de variables différents.

Voici les expressions mathématiques des différentes métriques propres à la régression:

• \(y_i\): Valeur réelle (observée) pour l’exemple numéro \(i\)
• \(\hat {y}_i\): Valeur prédite par le modèle pour l’exemple numéro \(i\)
• \(\bar {y}\): Moyenne des valeurs réelles : \(\bar {y}=\frac{1}{n}\sum _{i=1}^ny_i\)
• \(n\): Nombre total d’exemples (ou d’observations)