Exemple de régression linéaire simple avec NumPy, scikit-learn et Matplotlib

Objectif de cette leçon

Après avoir vu les grandes lignes du fonctionnement d’un modèle de Machine Learning à travers quelques équations mathématiques, nous allons maintenant adopter une approche concrète. L’objectif est de comprendre, par la pratique, comment une machine apprend à prédire à partir de données en suivant les étapes clés du processus d’apprentissage supervisé. Donc, Plutôt que d'utiliser des équations complexes, nous allons explorer un exemple simple de régression linéaire avec une seule variable. Nous allons donc apprendre à prédire le prix d’une maison en fonction de sa superficie.

Ce sera l’occasion de découvrir, au fil de l’exemple, les outils essentiels de l’écosystème Python pour l’apprentissage automatique, comme NumPy pour manipuler les données, scikit-learn pour entraîner un modèle et Matplotlib pour visualiser les résultats.

Prédire le prix d'une maison en fonction de sa superficie

Comprendre le scénario

Imaginez que vous soyez agent immobilier. Vous disposez d’un tableau regroupant les ventes récentes de maisons dans un quartier. Pour chacune d'entre elle, vous connaissez la superficie et le prix de vente. Très vite, vous remarquez une tendance: plus la maison est grande, plus elle est chère. Vous vous dites alors: «Et si je pouvais estimer le prix d’une maison simplement à partir de sa superficie?». C’est exactement ce que fait une machine lorsqu’elle apprend à prédire. Elle observe des exemples, repère des régularités et construit un modèle capable de généraliser à de nouveaux cas.

Nous allons explorer cette démarche à travers un exemple simple de régression linéaire avec une seule variable descriptive (la superficie dans ce cas). Ce type de régression est appelé régression univariée, car le modèle s’appuie sur une seule caractéristique (ou feature) pour faire ses prédictions.

Environnement de travail

Je rappelle que dans ce cours, nous allons travailler dans un environnement interactif appelé Jupyter Notebook, intégré à la distribution Anaconda. Cet outil est particulièrement adapté à l’apprentissage du machine learning, car il permet d’exécuter le code étape par étape, d’afficher les résultats directement sous les cellules et d’ajouter des explications textuelles entre les blocs de code. C’est un excellent support pour expérimenter, visualiser et comprendre le fonctionnement des modèles.

Importation des bibliothèques essentielles

Avant de commencer, nous allons importer les bibliothèques essentielles qui nous accompagneront tout au long de cet exemple, notamment, NumPy, Matplotlib et scikit-learn:
Voici une explication rapide des différents modules importés:

• NumPy: qu'on a abrégé np lors de l'importation, permet de créer et manipuler efficacement des tableaux numériques, ce qui est idéal pour représenter nos superficies et nos prix
• Matplotlib.pyplot: abrégé en plt est utilisé pour tracer des graphiques, afin de visualiser la relation entre les variables et les targets ainsi que les prédictions du modèle
• LinearRegression: issu de sklearn.linear_model (scikit-learn), est l’outil qui nous permettra d’entraîner un modèle de régression linéaire.
• mean_squared_error et r2_score: sont deux fonctions d’évaluation qui nous aideront à mesurer la qualité des prédictions du modèle par rapport aux données réelles. Bien entendu, il existe d'autres fonctions qui implémentent MAE et RMSE aussi.

         

Le dataset - Préparer les données d'entrainement

Dans la pratique, lorsqu’on développe un modèle de machine learning, on travaille à partir de datasets réels qui consistent en des fichiers structurés contenant des centaines ou des milliers d’exemples issus du monde concret (ventes immobilières, données médicales, comportements d’utilisateurs, etc.). Mais pour bien comprendre la logique d’apprentissage, il est souvent plus efficace de commencer par un exemple simple et contrôlé. C’est pourquoi, dans cette leçon, nous allons générer manuellement un petit jeu de données (juste quelques paires de valeurs représentant la superficie d’une maison et son prix). Cela nous permettra de nous familiariser avec les étapes clés du processus, comme la préparation des données, l'entraînement du modèle, la prédiction et la visualisation.
         
Imaginons que notre dataset est structuré de cette façon:

• La superficie, que l'on représente à l'aide d'une liste Python comme ceci:
  [30, 50, 70, 90, 110, 130, 150]
• Le prix, également représentée sous forme d'une liste:
  [100, 140, 220, 240, 290, 360, 400]

Il est essentiel que les données soient structurées dans un format compatible avec les bibliothèques utilisées, en particulier scikit-learn qui attend des tableaux bien définis pour fonctionner correctement. Une mauvaise organisation peut entraîner des erreurs lors de l’entraînement ou de la prédiction.

On aura donc le code suivant:
La méthode np.array() permet de créer un tableau numérique (tableau NumPy) à partir d’une liste de valeurs. Contrairement aux listes Python classiques, les tableaux NumPy sont optimisés pour les calculs scientifiques, notamment les opérations vectorielles, les transformations de forme et le fon fonctionnement avec les bibliothèques comme scikit-learn.

Dans notre exemple, np.array([30, 50, 70, ...]) crée un tableau structuré représentant les superficies que l’on peut ensuite facilement manipuler, visualiser ou utiliser pour entraîner un modèle.

La méthode reshape(-1, 1) de NumPy est utilisée pour changer la forme d’un tableau. En effet, elle permet de transformer un tableau 1D en une matrice 2D afin que la forme de données soit compatible avec les bibliothèques scikit-learn. Voilà ce qu'elle fait:

• L'argument -1 indique à NumPy de calculer automatiquement le nombre de lignes en fonction des données disponibles.
• L'argument 1 signifie que l’on veut une seule colonne

Par conséquent, la variable superficies devient une matrice 2D comme ceci: [[ 30],[ 50],[ 70],[ 90],[110],[130],[150]].

Pareil pour la variable prix que l'on transforme en tableau NumPy, mais sur une dimension seulement (donc pas la peine d'utiliser la méthode reshape).

Visualisation de données

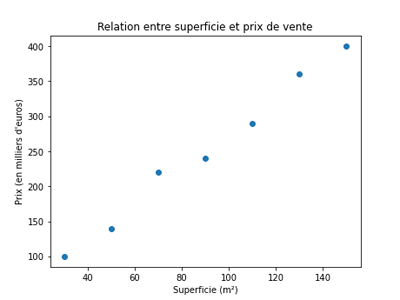
Visualiser les données est une étape essentielle avant d’entraîner un modèle. Cela permet de repérer rapidement les tendances, les anomalies ou les relations entre les variables. Dans notre cas, un simple nuage de points nous aidera à voir comment le prix varie en fonction de la superficie. C’est une première intuition visuelle avant toute modélisation.

Nous allons générer notre nuage de points avec matplotlib comme ceci:
Je pense que le code est assyez parlant, mais expliquons quand même les différentes instructions:

• plt.scatter(): affiche les points sur le graphique
• plt.xlabel() et plt.ylabel(): ajoutent les noms des axes
• plt.title(): ajoute un titre au graphique
• plt.show(): affiche le graphique dans Jupyter Notebook

Après exécution, on aura l'illustration suivante:
   

Entrainement du modèle

C'est sûrement l'étape que l'on attend depuis le début. En effet, c'est là où on apprendra le modèle à partir des données de notre dataset.

Le code d'entrainement et d'évaluation ressemblera à ceci:
Vous avez certainement remarqué que le code est particulièrement simple vue la nature de la tâche. En effet, la bibliothèque scikit-learn prend en charge toute la complexité mathématique que nous avons explorée dans le cours précédent, ce qui nous permet de nous concentrer sur la logique générale du modèle.

Expliquons rapidement les différents instructions:

• model=LinearRegression(): crée une instance du modèle de régression linéaire fourni par la bibliothèque scikit-learn. À ce stade, le modèle (qu'on a appelé model) est vide, c'est à dire qu'il n’a pas encore appris à partir des données. Donc le fait de l'utiliser pour faire des prédictions donnera des résultats tout à fait arbitraires.
• model.fit(superficies,prix): entraîne le modèle en lui fournissant les données d’entrée (superficies) et les valeurs cibles (prix). Le modèle va chercher à ajuster une droite qui minimise l’erreur entre les prédictions et les valeurs réelles (comme on l'a vu dans le leçon précédente).
• model.score(superficies,prix): évalue les performances du modèle sur les mêmes données. Cette méthode retourne le coefficient de détermination R², qui mesure la qualité de l’ajustement. Plus il est proche de 1, plus le modèle explique bien la variation des prix en fonction des superficies.

Le score obtenu est à peu près égal à 0.99. Cela signifie que 99% de la variation du prix est expliquée par la superficie, ce qui indique que le modèle de régression linéaire est très performant dans ce cas.
         

Prédictions et traçage de la rourbe de régression

Nous allons voir comment faire des prédictions sur des données. Dans notre cas, on utilisera les même données de superficies qu'on a utilisé pour l'entrainement afin de produire la droite de régression.

On exécute l'instruction suivante:
Cette instruction utilise le modèle entraîné pour prédire les prix en fonction des superficies données. Concrètement, model.predict(superficies) applique la droite de régression apprise aux valeurs de superficie et stocke les résultats dans prix_predit. Ce sont les prix estimés par le modèle pour chaque maison.

Maintenant, nous allons tracer le nuage de points de tout à l'heure, en plus de la droite de régression qui correspond à prix_predit pour visualiser l’ajustement du modèle par rapport aux données observées:
Cette fois, on a jouté la méthode plot() qui trace une courbe (et non pas des points). On l'a coloré ensuite avec du rouge (c="red") afin de distinguer la courbe de régression.

On aura l'illustration suivante:
   
On constate que la droite de régression est très bien ajustée au nuage de points qui représentent les données réelles, ce qui signifie que notre modèle est très performant.

Evaluer le modèle avec des métriques supplémentaires

En appelant la méthode score(), nous avons évalué notre modèle à l’aide du coefficient de détermination R². Toutefois, il existe d’autres métriques utiles pour mesurer la qualité d’un modèle de régression, comme la MAE, la MSE ou la RMSE.

Maintenant, nous allons utiliser les fonctions MSE et R² que nous avons déjà importées en début de programme:
Après exécution on aura:

MSE=113.77551020408175 et R2=0.9889076800636689

Expliquons rapidement ces résultats:

• MSE (Mean Squared Error) = 113.78 est l’erreur quadratique moyenne entre les prix réels et les prix prédits. Plus cette valeur est faible, plus les prédictions sont proches des observations.
• R² (coefficient de détermination) = 0.9889 signifie que 98.89% de la variation du prix est expliquée par la superficie. C’est un excellent score, indiquant que le modèle est très bien ajusté aux données.