Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications






Leçon 9: Régression linéaire multiple avec les DataFrames de Pandas
Toutes les leçons 

Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications
Leçon 9
Régression linéaire multiple avec les DataFrames de Pandas
Régression linéaire multiple avec les DataFrames de Pandas
Régression linéaire multiple (ou multivariée)
Qu'est ce qu'une régression multiple?
La régression linéaire multiple (ou multivariée) est une extension de la régression linéaire simple. Elle vise à prédire une variable cible \(Y\) à partir de plusieurs variables explicatives \(X_1\), \(X_2\),...,\(X_n\).Le modèle prend la forme suivante:
\(Y=\beta _0+\beta _1X_1+\beta _2X_2+\dots +\beta _pX_p\)
- \(\beta _0\): constante qui représente l'ordonnée à l’origine ou intercept (aussi connue sous le nom de biais).
- \(\beta _i\): coefficients de régression associés à chaque variable explicative
Lors de son apprentissage, le modèle de régression linéaire multiple cherche à estimer les coefficients optimaux (ainsi que le biais) qui minimisent l’écart entre les valeurs observées et les valeurs prédites. Ces éléments ajustés sont appelés paramètres du modèle.
Dataset fetch_california_housing pour apprendr à prédire les prix de maisons
Le dataset fetch_california_housing est un jeu de données fourni par la bibliothèque scikit-learn, issu du recensement californien de 1990. Il regroupe des informations socio-démographiques et géographiques sur différents quartiers de Californie.L'objectif principal du dataset fetch_california_housing consiste à prédire du prix médian des maisons. Chaque observation correspond à un quartier et inclut des variables telles que le revenu médian, l’âge moyen des habitations, le nombre moyen de pièces et d’occupants, ainsi que la latitude et la longitude. Ce dataset est couramment utilisé pour des exercices de régression, notamment pour tester des modèles prédictifs et explorer les relations entre facteurs économiques et prix de l’immobilier.
Nous allons voir comment afficher les informations concernant ce dataset quand on l'aura chargé dans Jupyter Notebook.
Prédire le prix de maisons à partir de plusieurs features
Chargement des modules
Comme pour la leçon précédente sur la régression linéaire simple, nous commençons par importer les modules nécessaires au fonctionnement de notre code.Les instructions d'importation auront cette forme:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, root_mean_squared_error
from sklearn.datasets import fetch_california_housing
Vous avez certainement reconnu les modules NumPy, matplotlib et scikit-learn. En effet, on les utilise souvent dans les projet de data science. Quant aux métriques, cette fois on va opter pour le MAE et le RMSE (en plus du R² bien entendu).
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_absolute_error, root_mean_squared_error
from sklearn.datasets import fetch_california_housing
Ce qui est nouveau cette fois c'est tout le module pandas qu'on a abrégé pd et le dataset fetch_california_housing fourni par scikit-learn (à travers le sous-module datasets).
Manipuler les données sous forme de DataFrames avec Pandas
Pandas est une bibliothèque incontournable en Python pour la manipulation et l’analyse de données. Elle introduit la structure appelée DataFrame, qui permet de représenter les données sous forme de tableau à deux dimensions, avec des lignes et des colonnes étiquetées (un peu comme une feuille Excel).L'organisation en données tabulaires facilite grandement l’exploration, le filtrage, le nettoyage et la visualisation des données. Grâce aux DataFrames, il devient intuitif de traiter des jeux de données complexes, d’effectuer des opérations statistiques ou de préparer les données pour des modèles de machine learning.
Pandas est construit sur la bibliothèque NumPy dont il hérite les performances et les structures de données sous-jacentes. Ses objets principaux, comme les Series et les DataFrames, reposent sur des tableaux NumPy pour le stockage et le traitement des données. Ainsi, toute manipulation de colonnes numériques dans un DataFrame exploite implicitement les fonctionnalités vectorisées de NumPy (même sans l’importer ou l’utiliser directement dans le code).
En Pandas, une Series est une structure de données unidimensionnelle similaire à une colonne d’un tableau ou d’un fichier Excel, mais enrichie de fonctionnalités puissantes, comme l'application des opérations vectorisées (somme, moyenne, filtrage…). Pour faire simple, une Series est une colonne dans un DataFrame.
Vous vous demandez sûrement à quoi bon d'importer NumPy puisque Pandas l'utilise implicitement. En fait, c'est juste par précaution, car il est possible d'en avoir besoin plus loin dans le code, comme pour changer les dimensions d'un vecteur avec reshape().
Explorer le dataset fetch_california_housing avec Pandas
Commençons par charger le jeu de données California Housing depuis la bibliothèque scikit-learn:data = fetch_california_housing()
L’objet data qui a été retourné est un objet de type Bunch, qui est une structure spécifique à scikit-learn très similaire aux dictionnaires Python. Donc si on affiche l'objet data, on aura quelque chose qui ressemble à ceci:
{
'data': DataFrame avec les variables explicatives (features),
'target': Series avec la variable cible (prix médian des maisons),
'frame': DataFrame combinant data et target,
'feature_names': ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude'],
'target_names': ['MedHouseVal'],
'DESCR': 'Description du dataset'
}
Il est recommandé d'afficher la description du dataset afin d'avoir une idée plus approfondie sur la structure et la nature des données. Nous allons donc afficher la clé DESCR comme ceci:
'data': DataFrame avec les variables explicatives (features),
'target': Series avec la variable cible (prix médian des maisons),
'frame': DataFrame combinant data et target,
'feature_names': ['MedInc', 'HouseAge', 'AveRooms', 'AveBedrms', 'Population', 'AveOccup', 'Latitude', 'Longitude'],
'target_names': ['MedHouseVal'],
'DESCR': 'Description du dataset'
}
data.DESCR
Ou bien comme ceci:
data["DESCR"]
En effet, le Bunch retourné par fetch_california_housing() se comporte à la fois comme un dictionnaire (data["DESCR"]) ou un objet avec attributs (data.DESCR).
Ensuite, nous allons exécuter les instructions suivantes et qui permettent de générer les features et le target à partir du dataset:
X = pd.DataFrame(data.data, columns=data.feature_names)
y = data.target
Je pense que vous avez compris l'instruction y = data.target. Elle sert à juste à créer une variable y qui constitue nos targets à partir de la clé target de l'objet data. Par contre, l'instruction précédente mérite une petite explication.
y = data.target
En effet, l'instruction en question permet de transformer les données explicatives du dataset California Housing en un tableau structuré avec Pandas. Elle crée un DataFrame nommé X, dont les colonnes sont nommées à partir de data.feature_names (qui renferme les noms des colonnes du dataframe) et dont les valeurs proviennent de data.data.
A la fin, les deux objets X et y générés, forment le couple classique features et target utilisé pour entraîner notre modèle de régression multiple.
L’argument feature_names sert à nommer explicitement les colonnes d’un tableau de données lorsqu’on le convertit en DataFrame Pandas. Il est particulièrement utile lorsqu’on crée un DataFrame à partir d’un tableau NumPy ou d’un jeu de données brut afin d’associer à chaque colonne un nom descriptif plutôt qu’un simple indice numérique.
Si vous voulez avoir un perçu sur la structure de nos factures, exécutez l'instruction suivante:
X.head()
On aura quelque chose qui ressemble à ceci:
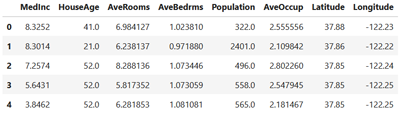
Par défaut, les 5 premières lignes de notre dataset (features) seront affichées. Si vous voulez un nombre différent de ligne, il suffit de l'expliciter entre les parenthèses de la méthode (par exemple X.head(10)).
Il sera également utile d'exécuter la méthode describe() qui permet de résumer statistiquement les colonnes numériques d’un DataFrame (ou d’une Series). Elle fournit un aperçu rapide des principales mesures statistiques, ce qui est très utile pour l’analyse exploratoire des données (EDA).
X.describe()
Après exécution on aura ceci:
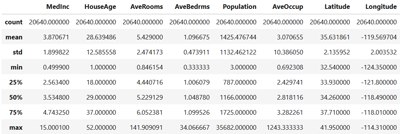
La méthode describe() affiche des mesures clés comme le nombre de valeurs (count), la moyenne (mean), l’écart-type (std), les valeurs minimales et maximales, ainsi que les quartiles (25%, 50% et 75%).
On peut aussi tracer des graphiques qui illustrent les correlations entre les données de notre dataset. Par exemple, la relation entre le revenu des habitants et le prix des logements dans les districts californiens.
On peut donc exécuter ce code:
plt.scatter(X.MedInc,y)
Ce qui donnera le graphique suivant:
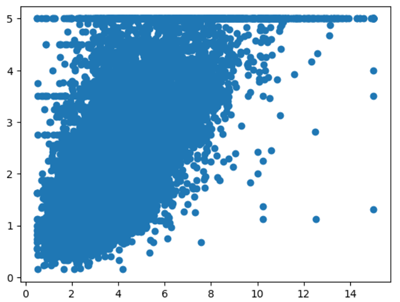
J'ai utilisé un code basique sans titre de graphique ni labels des axes. Cependant, vous pouvez améliorer l'illustration en suivant les étapes que nous avons vu lors de la leçon précédente.
On peut avoir le même résultat en exécutant ce code:
plt.scatter(X.iloc[:,0],y)
L'expression X.iloc[:, 0] sélectionne la première colonne de X (c’est-à-dire MedInc). En effet, iloc[]est une méthode de Pandas qui permet d’accéder aux éléments d’un DataFrame ou d’une Series par leur position (indice numérique) et non par leur nom.
L'expression X.iloc[:, 0] inclut le numéro de ligne et le numéro de colonne. Pour le numéro de ligne, on a appliqué le slicing (une technique très populaire en Python) pour désigner toute les lignes. Tandis qu'on a spécifié 0 pour le numéro de colonne, pour désigner la première colonne du dataframe.
Entrainement et évaluation du modèle
Nous allons maintenant entraîner notre modèle de régression linéaire multiple. Même si cette fois-ci nous utilisons plusieurs variables explicatives, le processus reste similaire à celui de la leçon précédente. En effet, la bibliothèque scikit-learn s’occupe de gérer cette complexité automatiquement.Nous allons donc exécuter ces instructions (les mêmes qu'avant):
model = LinearRegression()
model.fit(X, y)
model.score(X,y)
Ces trois instructions permettent respectivement de charger, entraîner et évaluer un modèle de régression linéaire multiple avec scikit-learn.
model.fit(X, y)
model.score(X,y)
La variable X englobe cette fois toutes les variables explicatives de notre dataset (d'où la régression multiple). En effet, La bibliothèque scikit-learn gère automatiquement les calculs matriciels, ce qui permet d’entraîner un modèle de régression linéaire multiple sans modifier le code quel que soit le nombre de variables explicatives. En interne, elle applique des opérations vectorielles optimisées pour estimer les coefficients du modèle, ce qui rend l’entraînement aussi simple avec une seule feature qu’avec plusieurs.
Le score retourné par model.score(X, y) correspond au coefficient de détermination R², une mesure statistique qui évalue la qualité de la prédiction d’un modèle de régression. Il indique la proportion de la variance de la variable cible y qui est expliquée par les variables explicatives X.
Pour cet exemple, le score R² est égal à 0.61, ce qui signifie que 61% de la variabilité des prix des maisons est expliquée par les variables du modèle (revenu médian, âge des maisons, densité, etc.). Cela suggère que le modèle capte une part significative de l’information, mais qu’il reste 39 % de variance non expliquée. C'est probablement liée à d’autres facteurs non inclus dans les données (comme la proximité et la qualité des écoles, la criminalité...).
On peut aussi calculer les performance en utilisant les métriques MAE et RMSE. Pour cela, il faut générer les prédictions que l'on stockera dans y_pred (exactement comme la leçon précédente):
y_pred = model.predict(X)
mae = mean_squared_error(y, y_pred)
rmse = root_mean_squared_error(y, y_pred)
print(f"MAE : {mae:.4f} - RMSE : {rmse:.4f}")
mae = mean_squared_error(y, y_pred)
rmse = root_mean_squared_error(y, y_pred)
print(f"MAE : {mae:.4f} - RMSE : {rmse:.4f}")
Les expressions {mae:.4f} et {rmse:.4f} invoquent une formule de formatage en Python utilisée pour afficher un nombre flottant (float) avec 4 chiffres après la virgule.
L'exécution du code précédent affiche:
MAE : 0.5243 - RMSE : 0.7241
Ces deux indicateurs mesurent l’erreur entre les prédictions du modèle et les valeurs réelles. Le MAE (Mean Absolute Error) de 0.5243 indique que, en moyenne, les prédictions s’écartent des valeurs réelles de 0.5243 unités (centaines de milliers de dollars dans ce cas, ce qui correspond à correspond à 52 000 dollars). Le RMSE (Root Mean Squared Error) de 0.7241 donne une mesure plus sensible aux grandes erreurs car il élève les écarts au carré avant de les moyenner.
Un RMSE plus élevé que le MAE suggère la présence de quelques erreurs importantes dans les prédictions. Ces valeurs permettent d’évaluer la précision globale du modèle. Dans le contexte du prix des maisons, cela signifie que le modèle a du mal à prédire correctement les valeurs très élevées (les maisons les plus chères).
Comme pour l'exemple de la leçon précédente sur la régression linéaire simple, nous avons évalué le modèle sur les mêmes données utilisées pour son entrainement, ce qui pourrait gonfler considérablement les métriques de performances. Nous verrons dans la leçon suivante comment séparer les données d'entrainement et de test.
Extraction des coefficients et de l'intercept d’un modèle
Après l'entraînement d’un modèle de régression, il devient possible d’accéder aux paramètres calculés qui traduisent la relation entre les variables explicatives (features) et la variable cible (target). Ces paramètres incluent notamment les coefficients associés à chaque variable notées \(\beta _i\) (pour \(i\) allant de 1 jusqu'à 8, vu qu'on dispose de 8 features), qui quantifient leur influence respective sur la prédiction, ainsi que l’intercept noté \(\beta _0\), représentant la valeur prédite lorsque toutes les variables sont nulles.L'identification de ces éléments permet non seulement d’interpréter le modèle, mais aussi de valider sa cohérence avec les attentes théoriques ou empiriques du domaine étudié.
Pour extraire ces paramètres, on fait appel aux attributs coef_ et intercept_ comme ceci:
model.coef_
Ce qui donne:
[ 4.36693293e-01, 9.43577803e-03, -1.07322041e-01, 6.45065694e-01, -3.97638942e-06, -3.78654265e-03, -4.21314378e-01, -4.34513755e-01 ]
et:
model.intercept_
Ce qui donne:
-36.941920207184396
Leçon 9
Régression linéaire multiple avec les DataFrames de Pandas
Régression linéaire multiple avec les DataFrames de Pandas


