Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications






Leçon 11: Régression linéaire multiple avec découpage des données en train set et test set
Toutes les leçons 

Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications
Leçon 11
Régression linéaire multiple avec découpage des données en train set et test set
Régression linéaire multiple avec découpage des données en train set et test set
Régression linéaire multiple en ségmentant les données en train set et test set
Dataset US Health Insurance
Le dataset US Health Insurance, fréquemment appelé "Medical Cost Personal Dataset", contient des informations sur des individus aux États-Unis et est utilisé pour prédire les frais médicaux engagés par les compagnies d’assurance en fonction de caractéristiques individuelles des assurés. Il est souvent employé dans des exercices de régression linéaire.Vous pouvez télécharger le dataset US Health Insurance depuis Kaggle.
Le dataset est constitué des champs suivants:
- age: Âge de l'individu
- sex: Sexe de l'individu (male ou female)
- bmi: Indice de masse corporelle. Il s'agit d'une mesure utilisée pour évaluer la corpulence d’un individu à partir de son poids et de sa taille.
- children: Nombre d’enfants à charge
- smoker: Statut tabagique (yes pour désigner fumeur ou no pour non fumeur)
- region: Région géographique où réside l'individu (northeast, southeast...)
- charges: Frais médicaux facturés (ce champs constitue la cible à prédire)
Elaboration du modèle de régression en ségmentant les données du dataset avec train_test_split
On commence par importer les modules nécessaires pour la manipulation du dataset et de l'élaboration du modèle de régression:import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
Je pense que vous connaissez déjà la signification de chacune de ces instructions vu qu'on les a déjà utilisé de nombreuses fois avant cela. La seule nouveauté consiste à l'importation du module train_test_split pour pouvoir ségmenter les données en train set et en test set.
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import root_mean_squared_error
La prochaine étape consiste à charger notre dataset en utilisant la fonction read_csv de pandas:
data=pd.read_csv("C:/US_Health_Insurance_Dataset.csv")
La méthode read_csv la bibliothèque pandas permet de lire un fichier CSV et de le convertir en DataFrame qui est une structure tabulaire très pratique pour manipuler des données et qu'on a déjà eu l'occasion de voir dans une leçon précédente.
En plus de read_csv, il y a aussi read_excel, read_json, read_sql etc... chacune est adaptée à un format de données spécifique et qui sera ensuite converti en DataFrame.
L’environnement Jupyter Notebook intègre une fonctionnalité d’auto-complétion qui suggère les fonctions disponibles au fur et à mesure de la saisie.
Quant à l'argument passé à la fonction read_csv, il s'agit tout simplement du chemin du dataset (là où vous l'avez enregistré après le téléchargement).
La fonction read_csv dispose également d'arguments supplémentaires que l'on peut spécifier au besoin comme:
- sep: qui spécifie le séparateur utilisé dans le fichier CSV (par défaut ',').
- names: permet de spécifier manuellement les noms des colonnes du DataFrame, au lieu d’utiliser la première ligne du fichier CSV comme en-tête.
- usecols:permet de sélectionner uniquement certaines colonnes à importer depuis un fichier CSV. C’est très utile pour gagner en performance et réduire la mémoire utilisée.
Jetons un coup d'oeil sur les cinq premières lignes de notre dataset:
data.head()
On obtient:
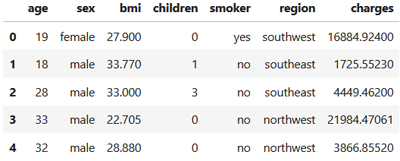
Vous avez sans doute remarqué que certaines colonnes comme sex, smoker ou region, contiennent des données catégorielles non numériques. Or, les algorithmes de régression manipulent des valeurs numériques pour établir des relations mathématiques entre les variables. Il est donc essentiel de convertir ces catégories en représentations numériques afin de permettre au modèle d’apprendre efficacement.
La prochaine étape consiste à convertir les valeurs non numériques en valeurs numériques dans les champs concernés. Nous allons donc exécuter ces instructions:
data["sex"]=data["sex"].apply(lambda x: 0 if x=="female" else 1)
data["smoker"]=data["smoker"].apply(lambda x: 0 if x=="no" else 1)
En effet, nous avons utilisé ce que l'on appelle une fonction anonyme pour effectuer cette opération.
data["smoker"]=data["smoker"].apply(lambda x: 0 if x=="no" else 1)
Une fonction anonyme (ou lambda function) est une fonction sans nom, définie en une seule ligne, souvent utilisée pour des opérations simples et ponctuelles. Une fonction anonyme respecte cette forme: lambda x: expression, où x est l’argument qu'on lui passe et expression est ce que la fonction retourne.
Donc, pour la première instruction:
data["sex"]=data["sex"].apply(lambda x: 0 if x=="female" else 1)
- data["sex"]: sélectionne la colonne sex du DataFrame data
- apply(): une méthode de pandas qui applique une fonctin à chaque valeur de la colonne à laquelle elle est associée.
- lambda x: 0 if x == "female" else 1 : transforme "female" en 0 et tout le reste (donc "male") en 1. L'argument x représente la valeur courante de la colonne sex, c’est-à-dire chaque cellule individuelle de cette colonne, lue une par une.
Pareil pour le champs smoker où 'yes' est remplacé par 1 et 'no' par 0.
Affichons à nouveau les cinq premières lignes de notre dataset:
data.head()
On obtient:
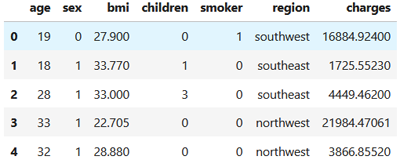
Vous vous dites sûrement pourquoi nous n'avons pas transformé le champe 'region' aussi, puisqu'il n'est pas numérique. En effet, nous allons carrément exclure ce champs des données de l'entrainement. Il s'agit normalement d'une opération qui s'inscrit dans le cadre du feature selection que nous allons voir plus loin. Pour le moment on se contentera des autre champs.
Il est temps de créer nos données X et y à partir du dataset. Nous allons procéder ainsi:
X=data[["age","sex","bmi","children","smoker"]]
y=data[["charges"]]
Là on vient de sélectionner les features que l'on souhaite intégrer dans l'entrainement (les variable X et y).
y=data[["charges"]]
Plutôt que de créer la matrice des variables explicatives X en sélectionnant les feature voulue, il est possible de procéder en excluant les champs que l'on veut pas (dans ce cas: region et charges) comme ceci:
X=data.drop(["region","charges"], axis=1)
En effet, la méthode drop() permet de supprimer les lignes ou les colones d'un dataframe. Pour désigner si on souhaite supprimer les lignes on définit axis=0 et si on veut supprimer les colones, alors on définit axis=1.
L’argument axis dans pandas est utilisé pour spécifier la direction sur laquelle une opération doit s’appliquer, c'est à dire par lignes ou par colonnes. Il est courrament utilisé dans de nombreuses situations et on aura certainement l'occasion de la revoir plus tard.
Maintenant c'est au tour de l'opération que l'on attend depuis le début, la séparation des données d'entrainement et du test:
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.2)
Dans ce cas, on a consacré 80% des données pour l'entrainement et 20% pour le test.
Si on exécute:
X_train.shape
X_test.shape
On aura respectivement: (1070, 5) et (268, 5).
X_test.shape
Créons notre modèle de régression linéaire que l'on entraine sur le train set:
model=LinearRegression()
model.fit(X_train,y_train)
Maintenant, on l'avalue sur le test set. Nous allons utiliser la métrique R² à travers la méthode score():
model.fit(X_train,y_train)
model.score(X_test,y_test)
On obtient un score de: 0.786, ce qui signifie que le modèle explique 78,6% de la variance des frais médicaux (charges) à partir des variables comme age, sex, bmi, children et smoker. Il s'agit d'un bon score dans un contexte réel, surtout si les données sont bruitées ou complexes.
Calculons maintenant les performances de notre modèle à l'aide de la métrique RMSE:
y_pred=model.predict(X_test)
rmse=root_mean_squared_error(y_test,y_pred)
print(f"RMSE: {rmse:.3f}"
Cela affiche
rmse=root_mean_squared_error(y_test,y_pred)
print(f"RMSE: {rmse:.3f}"
RMSE: 5181.745
Cela signifie que qu'en moyenne, les prédictions du modèle s’écartent de 5181,745 unités monétaires (dollars dans ce cas) par rapport aux vraies dépenses médicales. Cette erreur moyenne est à relativiser selon l’échelle des charges afin de préciser si c'est un bon score ou pas. Pour celà, il faudra bien analyser les statistiques relatives au dataset et que l'on peut facilement calculer avec data.describe() comme on l'a vu dans une leçons précédente, mais on va s'en passer cette fois.
Faire une prédiction avec le modèle entrainé
Essayons de faire une prédiction à l'aide de notre model qu'on a déjà entrainé et évalué.Supposons que nous voulons estimer les charges médicale d'une jeune fille (sex=0) de 21 ans (age=21) non fumeuse (smoker=0) avec un indice de masse corporelle normal (bmi=23) et qui n'a pas d'enfants (children=0).
Nous allons exécuter ce code:
model.predict([[21,0,23,0,0]])
La prédiction résultante est 916.092 $.
Maintenant, changeons les caractéristiques de la personne. Par exemple un homme (sex=1) de 60 ans (age=60) fumeur (smoker=1) avec un indice de masse corporelle qui undique un surpoids (bmi=33) et qui a 2 enfants (children=2).
model.predict([[60,1,33,2,1]])
La prédiction résultante est 38 875.842 $.
La méthode predict() de scikit-learn accepte un tableau à deux dimensions comme entrée, même s’il n’y a qu’un seul échantillon à prédire.
Leçon 11
Régression linéaire multiple avec découpage des données en train set et test set
Régression linéaire multiple avec découpage des données en train set et test set


