k-NN: classification par voisinage sans apprentissage explicite

Définition et principe de fonctionnement de l'algorithme k-NN

k-Nearest Neighbors ou k-NN (qui signifie les k plus proches voisins) est un algorithme d’apprentissage supervisé utilisé pour la classification. Il est apprécié pour sa simplicité et son intuitivité. En effet, il ne construit pas de modèle explicite, mais prend ses décisions en comparant un nouvel exemple aux données déjà observées. Son principal atout est qu’il peut s’adapter à des formes de décision complexes en s’appuyant sur la structure locale des données.

Le principe du k-NN est le suivant: lorsqu’un nouvel exemple doit être classé, le modèle recherche les k exemples les plus proches dans les données d’entraînement, puis lui attribue la classe la plus fréquente parmi ces voisins.

Algorithme non paramétrique basé sur les distances

k-NN est un algorithme non paramétrique, ce qui signifie qu’il ne cherche pas à apprendre une fonction ou des paramètres à partir des données. Contrairement à la régression logistique qui ajuste des coefficients pour modéliser une frontière de décision entre les classes, k-NN ne construit aucun modèle, mais il conserve simplement les exemples d’entraînement en mémoire et les utilise pour faire des prédictions.

Lorsqu’un nouvel exemple doit être classé, k-NN recherche les k exemples les plus proches dans les données selon une mesure de distance. La classe majoritaire parmi ces voisins est alors attribuée à l’exemple. La distance euclidienne est la plus courante, mais d’autres distances comme Manhattan ou cosinus peuvent être utilisées selon le type de données.

Dans cette illustration, le cercle vert (le point à classer) est entouré de quatre voisins mis en évidence (ce qui correspond à k=4) dans l’algorithme k-NN. Le modèle prendra en compte ces quatre points pour déterminer la classe majoritaire (rouge) et effectuer la prédiction.
   
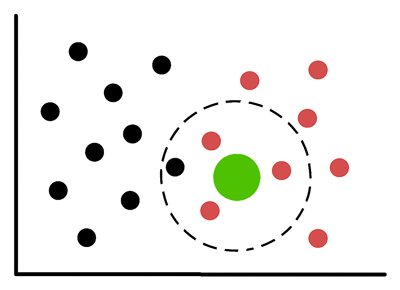
La dépendance à la distance rend l’algorithme k-NN sensible à l’échelle des variables et à la dimensionnalité. C'est pour cette raison qu'on est souvent amené à procéder à une bonne normalisation des variables.

Distance d'Euclide et distance de Manhattan

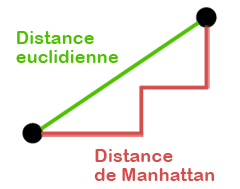
La distance euclidienne et la distance de Manhattan sont parmi les plus utilisées en k-NN, surtout dans les contextes classiques de classification supervisée.

La distance d'Euclide (ou distance euclidienne) est la distance "à vol d’oiseau" entre deux points dans l’espace. Elle mesure la longueur du segment droit qui les relie.

La distance entre deux point \(x\) et \(y\) représentées par les coordonnées \((x_1,x_2...), (y_1,y_2...)\) est exprimée par cette formule:
Cette distance est très utilisée quand les variables sont continues et normalisées. Elle fonctionne bien si toutes les dimensions ont une importance comparable.

La distance de Manhattan, quant à elle, simule le déplacement dans une ville quadrillée (comme Manhattan) où on ne peut pas couper à travers les blocs mais on avance horizontalement et verticalement.

La distance Manhattan est représentée par cette formule:
Cette distance est utile quand les variables sont discrètes ou quand les déplacements diagonaux n’ont pas de sens. Elle est aussi plus robuste aux valeurs extrêmes que la distance euclidienne.          
Cette illustratin montre deux points reliés par deux chemins différents: un segment droit pour la distance euclidienne (le chemin à vol d'oiseau et le plus court), et un chemin en escalier pour la distance de Manhattan (comme dans une ville quadrillée).
         

Comment choisir une valeur optimale de l'hyperparamètre k dans k-NN?

Le choix du bon k dans k-NN est crucial pour l’équilibre entre la précision et la robustesse. En effet, un k trop petit (par exemple k=1) rend le modèle très sensible au bruit, à titre d'exemple, un seul voisin erroné peut fausser la prédiction. Inversement, un k trop grand dilue l’influence locale et peut brouiller les frontières entre classes, surtout si les classes sont déséquilibrées.

Le paramètre k dans l’algorithme k-NN est ce qu’on appelle un hyperparamètre. Contrairement aux paramètres internes appris automatiquement par un modèle (comme les poids dans une régression logistique), un hyperparamètre est une valeur fixée manuellement avant l’entraînement.

En général, on détermine l'hyperparamètre k expérimentalement, souvent à l’aide de la méthode du coude (elbow method) ou par validation croisée.

• Validation croisée (cross-validation): On teste plusieurs valeurs de k sur des sous-ensembles des données et on choisit celle qui minimise l’erreur moyenne.
• Méthode du coude (elbow method): On trace l’erreur de classification en fonction de k. Le point où l’erreur cesse de diminuer significativement (le "coude") est souvent un bon choix.

         

Élaboration d’un k-NN pour la classification supervisée

Classification du dataset Iris avec k-NN

Comme dans les deux leçons précédentes, nous allons à nouveau utiliser le dataset Iris.

Cette fois-ci, le code sera présenté en un seul bloc, puisque vous en connaissez désormais ses différentes composantes:
Nous avons fixé l'hyperpamètre k à 3. Il s'agit d'un choix arbitraire mais fréquemment pertinent pour débuter.

Le code précédent affiche ce résulat:
         
Le modèle k-NN avec k=3 a obtenu une exéctitude parfaite (accuracy = 1.0) sur le jeu de test, ce qui signifie qu’il a correctement classé toutes les observations.

La matrice de confusion confirme cette performance (aucune erreur de classification entre les trois classes d’Iris). Ce résultat reflète une bonne séparation des classes dans les données. Néanmoins, il convient de rester prudent car une telle précision peut aussi indiquer un jeu de test trop simple ou les données de test sont trop proche des données d’entraînement.