Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications






Leçon 15: L'arbre de décision (decision tree): un outil puissant de classification
Toutes les leçons 

Intelligence artificielle et Machine Learning: méthodes, algorithmes et applications
Leçon 14
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
Leçon 15
L'arbre de décision (decision tree): un outil puissant de classification
L'arbre de décision (decision tree): un outil puissant de classification
Comprendre la classification avec les arbres de décision
Qu'est ce qu'un arbre de décision?
Un arbre de décision (ou decision tree) est un modèle d’apprentissage supervisé qui classe ou prédit en suivant une structure arborescente de questions. Il fonctionne en divisant les données étape par étape selon les caractéristiques les plus discriminantes, jusqu’à aboutir à une prédiction.On peut imaginer un arbre de décision comme une représentation graphique en forme d’arbre qui permet de prendre des décisions ou de faire des prédictions à partir de données. L'arbre est composé de:
- Nœud racine: Constitue le point de départ de l’arbre de décision. C’est à partir de ce nœud que l’algorithme commence à diviser les données. Il représente la première question posée sur une variable jugée la plus pertinente pour séparer les données.
- Nœuds internes: Sont les étapes intermédiaires de l’arbre. Chacun correspond à un test sur une variable (numérique ou catégorielle) qui permet de continuer à affiner la décision. Ces tests divisent les données en sous-groupes plus homogènes.
- Branches: Les branches relient les nœuds entre eux. Chaque branche correspond à une réponse possible au test posé dans le nœud parent. Dans le cas d’un test binaire, il y a généralement deux branches : une pour « oui » et une pour « non ».
- Feuilles: Sont les extrémités de l’arbre. Elles contiennent la prédiction finale faite par le modèle. Dans un problème de classification, chaque feuille correspond à une classe (par exemple : « achète » ou « n’achète pas »).
Cette illustration représente une forme simplifiée d'un arbre de décision:
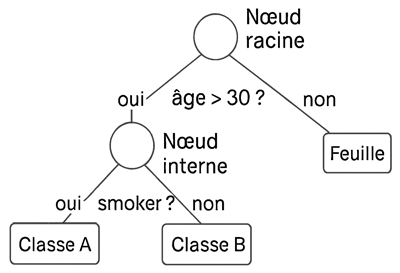
À l’instar de l’algorithme k-NN, les arbres de décision peuvent être appliqués aussi bien à des tâches de classification qu’à des problèmes de régression.
Comment fonctionne un arbre de décision?
La construction d’un arbre de décision repose sur un processus récursif qui vise à diviser les données en sous-groupes de plus en plus homogènes.Tout commence par le choix de la variable la plus pertinente pour séparer les données, selon un critère de pureté comme le gain d’information (utilisé par l’algorithme ID3) ou l’indice de Gini (utilisé par CART). Ce choix détermine le nœud racine qui pose une première question du type "âge > 30 ?" ou "couleur = rouge ?".
En fonction des réponses possibles, les données sont réparties dans des branches distinctes, chacune menant à un nouveau nœud où une autre variable est testée.
Ce processus se répète à chaque niveau de l’arbre, créant une structure hiérarchique où chaque embranchement affine la décision.
L’algorithme s’arrête lorsque les données d’un sous-groupe sont suffisamment homogènes (c’est-à-dire qu’elles appartiennent toutes à la même classe), ou lorsqu’un critère d’arrêt est atteint (comme une profondeur maximale ou un nombre minimal d’exemples). À ce stade, on atteint une feuille, qui contient la prédiction finale, c'est à dire une classe (dans le cas de la classification) ou une valeur (dans le cas de la régression).
Ainsi, l’arbre de décision fonctionne comme un système de questions-réponses qui guide progressivement vers une décision, en exploitant la structure des données pour maximiser la clarté et la précision des prédictions.
Les algorithmes derrière l’arbre de décision: ID3, C4.5 et CART
La construction d’un arbre de décision repose sur des algorithmes qui sélectionnent, à chaque étape, la variable la plus pertinente pour séparer les données.Parmi les algorithme les plus connus on trouve:
- ID3: qui utilise le gain d’information (une mesure basée sur l’entropie) pour choisir la caractéristique qui réduit le plus l’incertitude.
- C4.5: qui constitue une amélioration de ID3, introduit le gain de ratio et gère les variables continues ainsi que les données manquantes tout en intégrant un mécanisme d’élagage pour éviter le surapprentissage.
- CART (Classification and Regression Trees): se distingue par sa capacité à traiter aussi bien des problèmes de classification que de régression en s’appuyant sur l’indice de Gini pour évaluer l’impureté des nœuds.
Ces algorithmes déterminent la structure de l’arbre en posant successivement des questions qui orientent les données vers des feuilles de plus en plus homogènes, jusqu’à aboutir à une prédiction finale.
L’indice de Gini est une mesure d’impureté qui indique à quel point un nœud contient des éléments de classes mélangées. Si toutes les données appartiennent à une seule classe, alors Gini = 0 (pour désigner une pureté maximale). Si les classes sont parfaitement équilibrées, alors Gini est proche de 0.5 (pour désigner une impureté maximale pour deux classes).
Arbres de décision et séparation non linéaire des données
L’arbre de décision est particulièrement adapté aux données non linéairement séparables. En effet, il ne cherche pas à tracer une frontière globale dans l’espace des variables (comme la régression losigtique). Au lieu de cela, il segmente l’espace de manière hiérarchique et conditionnelle en posant des questions successives sur les caractéristiques des données (par exemple: « âge > 30 ? », puis « revenu < 40k ? »...). Chaque règle crée une coupure locale et l’enchaînement de ces règles permet de modéliser des relations complexes, même lorsque les classes ne sont pas séparables par une ligne droite ou un plan.Ainsi, même dans des cas où les données sont entremêlées de façon non linéaire, l’arbre peut isoler des zones pertinentes en combinant plusieurs conditions. Cette capacité à construire des frontières de décision en escalier rend l’arbre de décision très flexible.
Toutefois, plus la structure devient complexe, plus le risque de surapprentissage (overfitting) augmente, ce qui justifie souvent l’usage de méthodes ensemblistes comme les forêts aléatoires ou le boosting pour gagner en robustesse.
Les modèles ensemblistes tels que les forêts aléatoires (Random Forest) ou le Gradient Boosting, qui combinent plusieurs arbres pour améliorer la performance et la robustesse, ainsi que les techniques de régularisation pour contrer l'overfitting, seront abordés plus loin dans ce cours.
Implémentation d’un arbre de décision sur le dataset Titanic
Présentation du dataset Titanic
Le dataset Titanic contient des informations sur les passagers du célèbre paquebot ayant fait naufrage en 1912. L’objectif classique est de prédire si un passager a survécu ou non, en fonction de ses caractéristiques personnelles et de son contexte de voyage.Le dataset contient des variables telles que la classe du billet (Pclass), le sexe (Sex), l’âge (Age), le nombre de proches à bord (SibSp, Parch), le tarif payé (Fare) et le port d’embarquement (Embarked). La variable cible (Survived) indique si le passager a survécu (1) ou non (0).
Le dataset Titanic présente plusieurs valeurs manquantes, notamment dans les variables Age, Cabin et parfois Embarked. Ce problème de données incomplètes est courant dans les jeux réels et nécessite un prétraitement adapté avant l’entraînement d’un modèle. Selon le cas, on peut choisir de supprimer les lignes incomplètes ou d’imputer les valeurs manquantes à l’aide de la moyenne, de la médiane ou d’une valeur fréquente.
La gestion des données manquantes est une étape cruciale en data science, et nous aurons l’occasion d’en explorer les différentes stratégies (comme l'imputation, l'interpolation, le traitement conditionnel, etc.) plus loin dans ce cours. Pour l’instant, nous nous contenterons de supprimer les lignes incomplètes.
Téléchargement du dataset Titanic
Le dataset Titanic n’est pas inclus directement dans les bibliothèques comme scikit-learn (comme c'est le cas du dataset Iris), mais il est facilement accessible en ligne.L’une des sources les plus pratiques est le dépôt GitHub de Data Science Dojo, qui propose une version propre du fichier CSV.
Le dataset est également disponible sur Kaggle dans le cadre d’un célèbre concours d’apprentissage automatique.
Prédire la survie des passagers du Titanic avec un arbre de décision
Commençons par importer les bibliothèques requises et charger le dataset Titanic:import pandas as pd
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
df = pd.read_csv("titanic.csv")
Vous pouvez exécuter les instruction df.head() pour avoir un aperçu sur la forme du dataset. Vous pouvez aussi exécuter l'instruction df.describe() pour voir le nombre de champs (statistique count). Vous allez remarquer que ce nombre n'est pas le même partout, ce qui indique des valeurs manquantes.
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, plot_tree
from sklearn.metrics import accuracy_score, confusion_matrix
import matplotlib.pyplot as plt
df = pd.read_csv("titanic.csv")
On procède maintenant à un prétraitement basique de données:
df = df[["Survived", "Pclass", "Sex", "Age", "SibSp", "Parch", "Fare"]].dropna()
df["Sex"] = df["Sex"].map({"male": 0, "female": 1})
df["Sex"] = df["Sex"].map({"male": 0, "female": 1})
Le première instruction sélectionne les champs que l'on souhaite inclure lors du traitement. Il s'agit d'une opération que nous avons déjà fait avant. La méthode dropna() supprime les lignes qui présentent au moins une valeur manquante parmi ses champs.
La deuxième instruction du bloc transforme les valeurs "male" et "female" respectivement en 0 et 1. On appelle cette opération un encodage binaire. Il s'agit d'une opération que nous avons égalalement effectué auparavant, mais à travers la méthode apply() et la fonction anonyme lambda.
Ensuite, on sépare les variables explicatives de la cible à travers une opération qui nous est familière:
X = df.drop("Survived", axis=1)
y = df["Survived"]
Le reste du code est un classique de la classification:
y = df["Survived"]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
clf = DecisionTreeClassifier(max_depth=3, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Exactitude sur le jeu de test: {accuracy:.2f}")
cm=confusion_matrix(y_test,y_pred)
print(cm)
La nouveauté est l'utilisation du modèle d’arbre de décision avec deux paramètres importants:
clf = DecisionTreeClassifier(max_depth=3, random_state=42)
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
accuracy = accuracy_score(y_test, y_pred)
print(f"Exactitude sur le jeu de test: {accuracy:.2f}")
cm=confusion_matrix(y_test,y_pred)
print(cm)
- max_depth=3: limite la profondeur maximale de l’arbre à 3 niveaux. Cela agit comme une régularisation pour éviter le surapprentissage (overfitting) en empêchant l’arbre de devenir trop complexe.
- random_state=42: fixe la graine aléatoire pour garantir la reproductibilité des résultats. Cela permet d’obtenir le même découpage et le même arbre à chaque exécution.
L'exécution de ce bloc donne:
Exactitude sur le jeu de test: 0.74
[[ 72 15 ]
[ 22 34 ]]
[[ 72 15 ]
[ 22 34 ]]
D'après les résultats, 74 % des prédictions faites par l’arbre de décision sur les données de test sont correctes. C’est une mesure globale de performance, mais elle ne dit pas tout. C'est justement pour cela qu'on a aussi généré une matrice de confusion.
La matrice de confusion nous permet de voir où le modèle se trompe. Voilà une analyse des résultats:
- TN (True Negatives) = 72: le modèle a bien prédit que ces passagers n’ont pas survécu.
- FP (False Positives) = 15: le modèle a prédit à tort qu’ils ont survécu.
- FN (False Negatives) = 22: le modèle a prédit à tort qu’ils n’ont pas survécu.
- TP (True Positives) = 34: le modèle a bien prédit qu’ils ont survécu.
En résumé, le modèle est plutôt bon pour détecter les non-survivants (72 vrais négatifs), mais il a plus de mal à identifier correctement les survivants (22 faux négatifs). Donc, on pourrait envisager d’ajuster certains hyperparamètres du modèle ou d’utiliser d’autres métriques comme le rappel, la précision, ou le score F1 pour mieux évaluer la performance selon les objectifs.
Évaluer un modèle de classification avec la courbe ROC
La courbe ROC (Receiver Operating Characteristic) est un outil graphique utilisé pour évaluer les performances d’un modèle de classification binaire.La courbe ROC (ou ROC curve) trace le taux de vrais positifs en fonction du taux de faux positifs pour différents seuils de décision. Chaque point de la courbe correspond à un seuil donné, et montre le compromis entre sensibilité (capacité à détecter les positifs) et spécificité (capacité à éviter les faux positifs).
La courbe est constitué des éléments suivants:
- L’axe horizontal (FPR) représente le de faux positifs (proportion de non-survivants mal classés comme survivants).
- L’axe vertical (TPR) représente le taux de vrais positifs (proportion de survivants correctement identifiés).
- Chaque point sur la courbe correspond à un seuil de décision différent (de 0 à 1).
Comment lire le graphique?
Plus la courbe ROC s’élève rapidement vers le coin supérieur gauche, plus le modèle est performant pour distinguer les classes, tandis qu’une courbe proche de la diagonale indique un comportement quasi aléatoire. L’AUC (Area Under Curve), souvent affichée avec la courbe, résume cette performance. Plus elle est proche de 1, meilleure est la capacité du modèle à séparer les classes positives et négatives.
En général:
- AUC ≈ 0.5: modèle aléatoire
- AUC ≥ 0.7: modèle acceptable
- AUC ≥ 0.9: excellent modèle
Pour générer le ROC curve on exécute le code suivant:
from sklearn.metrics import RocCurveDisplay
RocCurveDisplay.from_estimator(clf, X_test, y_test)
plt.title("Courbe ROC - Arbre de décision")
plt.show()
Ce qui donne ce résultat:
RocCurveDisplay.from_estimator(clf, X_test, y_test)
plt.title("Courbe ROC - Arbre de décision")
plt.show()
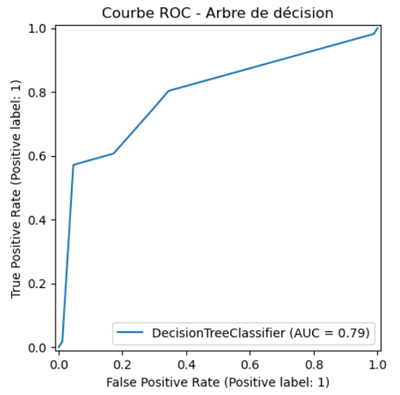
Donc, pour notre modèle qui affiche une courbe qui s’élève bien au-dessus de la diagonale avec une AUC de 0.79. On peut dire qu'il dispose d'une bonne capacité à distinguer les survivants des non-survivants (même si l'exactitude brute est de 0.74).
Leçon 14
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
k-Nearest Neighbors (k-NN): Algorithme de classification non paramétrique basé sur les distances
Leçon 15
L'arbre de décision (decision tree): un outil puissant de classification
L'arbre de décision (decision tree): un outil puissant de classification


