k-means: un algorithme central de l’apprentissage non supervisé

Qu'est ce que l'algorithme k-means?

k-means est un algorithme d’apprentissage non supervisé dont l’objectif est de regrouper des observations en un nombre fixé de groupes appelés clusters. Contrairement à l’apprentissage supervisé, il ne dispose d’aucune étiquette ou de classe prédéfinie. En effet, l'algorithme k-means analyse uniquement la structure interne des données pour identifier des ensembles d’éléments similaires. L’algorithme fonctionne en alternant deux étapes simples: attribuer chaque point au centre le plus proche, puis recalculer ces centres jusqu’à stabilisation. Le résultat final est une partition du jeu de données en k groupes cohérents, chacun représenté par un centroïde.

Pourquoi utiliser k-means?

k-means est particulièrement utile lorsqu’on souhaite révéler des structures cachées dans un dataset ou organiser les données en catégories naturelles sans connaissance préalable des classes. Il est largement utilisé pour segmenter des clients, regrouper des documents, analyser des comportements ou encore simplifier des données complexes en identifiant des profils types. Sa simplicité, sa rapidité et sa capacité à traiter de grands volumes de données en font un outil incontournable pour l’exploration initiale, la visualisation ou la préparation de modèles plus avancés. Pour résumer, k-means permet de transformer un ensemble de données brutes en une représentation plus lisible et exploitable.

Mode de fonctionnement de l'algorithme k-means

L’algorithme k-means repose sur l’idée de regrouper les données en k clusters, chacun représenté par un centroïde, c’est‑à‑dire un point fictif correspondant à la moyenne des observations du groupe.

Le processus commence par l’initialisation de k centroïdes (souvent choisis aléatoirement). Ensuite, l’algorithme alterne deux étapes:

• Affectation: Chaque observation est associée au centroïde le plus proche selon une mesure de distance (généralement la distance euclidienne qu'on a vu dans la leçon consacrée à l'algorithme k-NN).
• Mise à jour: Pour chaque cluster, le centroïde est recalculé comme la moyenne des points qui lui sont assignés.

Ces deux étapes se répètent jusqu’à ce que les centroïdes ne changent presque plus ou qu’un critère d’arrêt soit atteint. Le résultat final est une partition stable des données où chaque cluster est défini par un centroïde qui en représente la structure moyenne.

Mieux choisir les centroïdes pour de meilleurs clusters à l'aide de k-means++

La qualité du regroupement obtenu par k-means dépend fortement de la position initiale des centroïdes car la manière avec laquelle l'algorithme converge peut varier selon cette configuration de départ. Une mauvaise initialisation peut entraîner des clusters peu représentatifs, déséquilibrés ou sensibles au bruit. Pour améliorer la robustesse et la cohérence des résultats, une variante appelée k-means++ a été introduite.

L'algorithme k-means++ sélectionne les centroïdes initiaux de manière probabiliste en favorisant les points éloignés les uns des autres. Cette stratégie réduit les risques de convergence vers des solutions sous-optimales et permet d’obtenir des partitions plus stables et plus pertinentes, notamment dans les jeux de données complexes ou à forte variabilité.

Mise en oeuvre pratique de l'algorithme de clustring k-means

Jeu de données Mall Customers

Le dataset Mall Customers est un petit jeu de données très utilisé pour les exercices de segmentation client. Il contient 200 individus décrits par 5 variables: un identifiant unique du client, le genre, l’âge, le revenu annuel (exprimé en milliers de dollars) et un spending score (une note attribuée par le centre commercial pour représenter le comportement d’achat et le niveau de dépense du client).

Le dataset Mall Customers est particulièrement adapté aux méthodes de clustering comme k-means, car il permet d’identifier des groupes de clients aux profils similaires (par exemple jeunes à fort revenu, seniors à faible dépense, etc.) et d’explorer des stratégies de segmentation marketing basées sur les caractéristiques socio‑démographiques et les habitudes de consommation.

Vous pouvez télécharger le datast Mall Customers depuis Kaggle en suivant ce lien: https://www.kaggle.com/datasets/shwetabh123/mall-customers.

Implémentation du modèle k-means pour ségmenter les clients du dataset Mall Customers

On commence par importer les modules nécessaires au fonctionnement de notre code. On charge également le dataset à partir de l'emplacement où il a été enregistré:
Affichons les cinq premières lignes de notre dataset pour avoir une idée sur les champs qu'il contient:
On obtient:

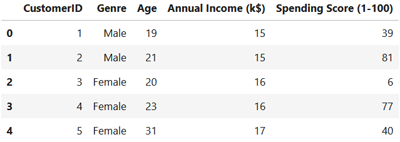
Pour simplifier la visualisation finale, on se contentera de sélectionner Annual Income et Spending Score parmi les champs du dataset:
Comme nous ne connaissons pas à l’avance le nombre optimal de clusters pour l’entraînement, nous allons utiliser la méthode du coude afin d’évaluer différentes valeurs de k. Le code suivant permet justement de calculer le WCSS (Within-Cluster Sum of Squares) pour plusieurs choix de k et d’identifier celui qui offre le meilleur compromis:
Le code précédent sert à évaluer la qualité du clustering pour différents nombres de clusters k afin d’identifier la valeur optimale à l’aide de la méthode du coude (Elbow Method).

La liste wcss stocke le Within-Cluster Sum of Squares, c’est‑à‑dire la somme des distances au carré entre chaque point et le centroïde de son cluster. Plus cette valeur est faible, plus les clusters sont compacts.

La boucle teste successivement k=1 à k=10 en entraînant un modèle k-means pour chaque valeur. L’option init="k-means++" garantit une meilleure initialisation des centroïdes et random_state=42 assure la reproductibilité de l'expérience.

Après chaque entraînement, kmeans.inertia_ (qui correspond au WCSS) est ajouté à la liste. En traçant ensuite wcss en fonction de k, on observe généralement un point où la diminution devient moins marquée. Ce point correspond au "coude" (elbow) qui indique le nombre de clusters le plus pertinent.

Après exécution du code, on obtient ce résultat:

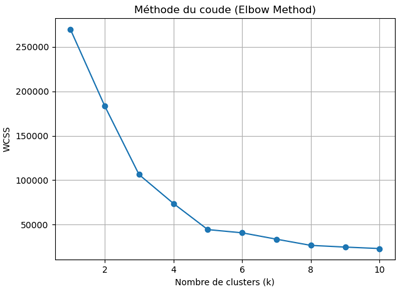
Le coude correspond à l’endroit où la baisse du WCSS devient nettement moins marquée. Dans notre cas, cette rupture apparaît autour de 5, ce qui indique que k=5 constitue le choix le plus pertinent pour le nombre de clusters lors de l'entrainement du modèle.

Il est temps d'entrainer notre modèle de clustering:
Ce code entraîne un modèle k-means avec 5 clusters en utilisant l’initialisation k-means++ pour choisir de meilleurs centroïdes de départ et un random_state pour garantir la reproductibilité.

La méthode fit_predict(X) réalise deux actions: elle apprend les clusters à partir des données X (phase fit) et attribue à chaque observation un numéro de cluster (phase predict). Le résultat ( qui est un vecteur contenant l’étiquette de cluster de chaque ligne) est ensuite stocké dans df["Cluster"], ce qui ajoute une nouvelle colonne au DataFrame avec le numéro du cluster auquel appartient chaque individu.

Maintenant, on visualise le résultat du clustering à travers ce code:
Le code précédent permet de visualiser la segmentation obtenue par k-means en représentant chaque client sous forme de point dans un plan défini par le revenu annuel et le spending score, avec une couleur différente pour chaque cluster identifié.

La fonction plt.scatter trace d’abord les individus en utilisant la variable clusters pour colorer les points selon leur groupe, ce qui permet de distinguer visuellement les segments formés. Ensuite, une seconde commande plt.scatter ajoute les centroïdes calculés par l’algorithme (accessibles via kmeans.cluster_centers_ qui contient les coordonnées moyennes de chaque cluster dans l’espace des variables utilisées). Ces centroïdes affichés en rouge et en forme de X, représentent le cœur de chaque groupe et permettent de visualiser la position moyenne des clients appartenant à chaque segment.

L'exécution du code produit ce résultat:


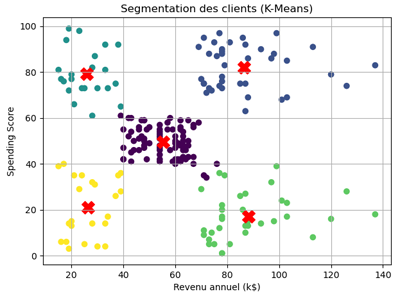
Ce graphique permet de visualiser clairement la segmentation des clients en montrant la structure des clusters et la manière dont ils se répartissent dans l’espace des caractéristiques.