Support Vector Machines (SVM)

Qu'est ce que le SVM?

Une machine à vecteurs de support (ou Support Vector Machines - SVM) est un modèle d’apprentissage supervisé qui consiste à séparer des données en différentes catégories de la manière la plus claire et la plus fiable possible.

Afin d'assurer une telle séparation, le modèle SVM construit une frontière de décision (decision boundary) qui peut prendre la forme d’une simple ligne dans un espace à deux dimensions, d’un plan en trois dimensions ou encore d’un hyperplan dans des espaces de dimension plus élevée. Cette frontière est définie de façon à laisser le plus grand espace (marge) possible entre les groupes de données. Les éléments situés au plus près de cette frontière, appelés vecteurs de support (support vectors), jouent un rôle central car ce sont eux qui fixent la position et l’orientation de la séparation.

En maximisant cette marge, le modèle gagne en robustesse et en capacité à généraliser, c’est-à-dire à bien classer de nouvelles données qu’il n’a jamais vues auparavant.

La figure suivante illustre la manière avec laquelle la frontièrte de décision (decision boundary) est placée après avoir maximisé la marge entre les vecteurs de support:

Mode de fonctionnement de l'algorithme SVM

L’algorithme des Support Vector Machines repose sur l’idée de séparer deux ensembles de données par une frontière de décision optimale. Chaque exemple du jeu de données est représenté par un vecteur de caractéristiques \(\mathbf{x_{\mathnormal{i}}}\), associé à une étiquette \(y_i\) qui vaut généralement -1 ou +1 selon la classe. Le rôle du SVM est de trouver un hyperplan, défini par l’équation qui sépare au mieux ces deux classes exprimée comme ceci:
Ici, \(w\) est un vecteur normal à l’hyperplan et il indique son orientation. Le paramètre \(b\) est un biais qui détermine son positionnement.

Pour que la séparation soit correcte, l’algorithme exige que les points d’une classe doivent se situer d’un côté de l’hyperplan et ceux de l’autre classe de l’autre côté. Mathématiquement, cela s’écrit:
Les points qui satisfont cette condition avec une égalité (c’est-à-dire ceux qui se trouvent exactement sur les marges) sont appelés vecteurs de support. Ce sont eux qui déterminent la position et l’orientation de l’hyperplan. Les autres points n’influencent pas directement la solution finale, même s'ils appartiennent au jeu de données.

La distance entre les deux marges est appelée marge et elle est donnée par la formule:
L’objectif du SVM est de maximiser cette marge. Plus elle est grande, plus la séparation est robuste et plus le modèle est capable de bien généraliser sur de nouvelles données. Maximiser la marge revient à minimiser \(\| w\| ^2\), ce qui transforme le problème en une tâche d’optimisation quadratique. L’algorithme résout donc un système d’équations et de contraintes pour trouver le vecteur \(w\) et le biais b qui définissent l’hyperplan optimal.

En résumé, l’hyperplan est placé exactement au centre des marges à la même distance des vecteurs de support de chaque classe. Ce placement est calculé par un processus d’optimisation qui cherche à maximiser la marge tout en respectant les contraintes de séparation. C’est cette rigueur mathématique qui confère aux SVM leur puissance et leur capacité à produire des modèles fiables, même dans des espaces de grande dimension.
         

Astuce du noyau (kernel trick)

L’astuce du noyau (kernel trick) permet aux SVM de gérer des données qui ne sont pas séparables par une simple ligne ou un plan dans leur espace d’origine. Plutôt que de chercher une séparation linéaire impossible, on utilise des fonctions noyaux qui projettent implicitement les données dans un espace de dimension supérieure où elles deviennent séparables.

Le noyau le plus utilisé est le RBF (Radial Basis Function) qui mesure la similarité entre deux points en fonction de leur distance. Concrètement, cela permet de tracer des frontières de décision courbes et flexibles capables d’épouser des formes complexes dans les données.

Grâce à l'astuce du noyau, le SVM conserve son principe fondamental qui consisste à maximiser la marge tout en s’adaptant à des situations où une séparation linéaire n’est pas suffisante.

Cette illustration montre (de manière simplifiée) comment les données ont été transformés à l'aide de l'astuce du noyau en utilisant RBF:

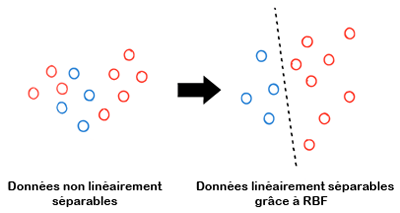
À gauche, les données ne sont pas linéairement séparables dans leur espace d’origine, tandis qu’à droite et grâce au noyau RBF, elles ont été projetées dans un espace où une séparation linéaire devient possible.      
   

Implémentation du SVM sur le dataset Titanic

Entrainement d'un modèle en utilisant un noyau linéraire

Je vous propose à nouveau le code intégral identique à celui étudié et détaillé dans la leçon précédente, à l’exception du modèle qui, cette fois sera un SVM.
La seule nouveauté dans ce code consiste à l'invocation du modèle SVC (Support Vector Classifier) qui fait référence à Support Vector Machines pour la classification.

Les arguments qu'on a passé au modèle sont:

• kernel="linear":Indique que le SVM doit utiliser un noyau linéaire. Cela signifie que le modèle cherche une séparation par une droite (ou hyperplan) dans l’espace original des données sans transformation implicite vers un espace de dimension supérieure.
• probability=True: Par défaut, le SVM ne fournit que des prédictions de classes (0 ou 1). Avec probability=True, il calcule aussi des probabilités associées aux prédictions, ce qui est utile si t on veut tracer une courbe ROC ou obtenir des scores de probabilité pour chaque classe.
• random_state=42:Fixe la graine aléatoire utilisée par certains processus internes comme la calibration des probabilités. Cela garantit que les résultats soient reproductibles si jamais on souhaite relancer le programme et avoir les mêmes résultats.

Après exécution, on obtient ceci:
L’interprétation de ces résultats ne devrait pas poser de difficulté, étant donné que nous l’avons déjà abordée à plusieurs reprises.          

Entrainement du modèle en utilisant un noyau RBF

Nons conservons le même code que l'on vient d'exécuter et on remplace seulement le kernel linéraire par RBF comme ceci:
On obtient cette fois:
Sur le dataset Titanic, le noyau RBF a atteint une exactitude de 0.62, tandis que le noyau linéaire a obtenu 0.73. Donc, le noyau linéaire semble mieux adapté car les variables du Titanic (classe, sexe, âge...) sont relativement simples et souvent corrélées de manière quasi linéaire avec la survie.
   
Vous pouvez également évaluer le modèle à l’aide d’autres métriques comme la précision, le rappel ou le score F1 et visualiser ses performances au moyen d’une matrice de confusion illustrée (sous forme d'image plus esthétique) ou d’une courbe ROC. Je pense que vous savez désormais comment procéder puisque nous l’avons vu auparavant.