DBSCAN: une approche de clustering basée sur la densité

Qu'est ce que l'algorithme DBSCAN et en quoi est-il différent de k-means?

Contrairement à k-means, qui regroupe les données en cherchant à minimiser la distance aux centroïdes et exige de fixer à l’avance le nombre de clusters, DBSCAN adopte une approche totalement différente fondée sur la densité. En effet, là où k-means impose des clusters de forme plutôt sphérique et sensibles aux valeurs aberrantes, DBSCAN identifie des zones où les points sont suffisamment proches les uns des autres pour former des régions denses sans présumer du nombre de groupes.

DBSCAN repose sur deux paramètres essentiels:

• \(ε\) (epsilon): C’est une distance maximale qui définit un rayon autour d’un point. Par exemple, si on imagine qu'on trace un petit cercle autour de chaque observation, alors tous les points qui tombent dans ce cercle sont considérés comme ses voisins.
• min_samples: Ce paramètre correspond au nombre minimal de voisins qu’un point doit avoir dans ce rayon \(ε\) pour être considéré comme suffisamment entouré.

La combinaison de ces deux paramètres permet à DBSCAN d’identifier les zones de forte densité et de distinguer les catégories des points. En effet, DBSCAN classe chaque observation en trois catégories:

• Core: Un point est dit core s’il possède au moins un certain nombre de voisins dans un rayon \(ε\), ce qui en fait le cœur structurel d’un cluster.
• Border: Un point border se trouve en périphérie, donc trop isolé pour être un core mais suffisamment proche d’un core pour appartenir au cluster.
• Noise: Un point noise est considéré comme du bruit car il ne se trouve dans aucune zone suffisamment dense.

Cette distinction permet à DBSCAN de détecter des clusters de formes arbitraires, de gérer naturellement les valeurs aberrantes et de ne pas imposer un nombre de clusters fixe (contrairement à k-means qui force chaque point à appartenir à un groupe même s’il est isolé).

Application de l’algorithme DBSCAN au dataset Mall Customers

Maintenant que vous maîtrisez la construction complète d’un pipeline de clustering (que nous avons illustrée avec k-means), je vais vous présenter le code final en une seule fois et je me concentrerai uniquement sur les éléments propres à DBSCAN.

Je propose ce code:
Je pense que vous savez déjà comment ce code fonctionne. Je vais juste m'arrêter sur cette instruction:

Ce code crée un modèle DBSCAN en fixant les deux paramètres essentiels expliqués précédemment:

• eps=5: Représente le rayon du voisinage \(ε\) autour d’un point. Concrètement, DBSCAN trace un cercle de rayon 5 autour de chaque point. Tous les points situés dans ce rayon sont considérés comme ses voisins. Plus eps est grand, plus les clusters seront larges et faciles à former.
• min_samples=5: Ce paramètre indique le nombre minimal de voisins qu’un point doit avoir dans le rayon eps pour être considéré comme un core point. Ici, un point doit avoir au moins 5 points dans son voisinage (lui inclus) pour être au cœur d’un cluster.

Donc, si un point a ≥ 5 voisins dans un rayon de 5 unités, il devient un core point. Les points proches d’un core point mais avec moins de voisins deviennent border points. Quant aux points trop isolés, ils deviennent noise (étiquetés par -1).

Le graphique résultant suite à l'exécution du code ressemble à ceci:


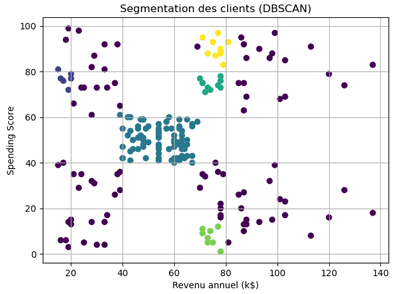
Si on veut une façon rapide de compter combien de points appartiennent à chaque cluster après l’application de DBSCAN (ou k-means, ou n’importe quel clustering), on peut ajouter cette instruction:
Celà donne:
Le résultat indique que DBSCAN a identifié plusieurs clusters de tailles très différentes, mais surtout qu’il a classé 87 points comme bruit (-1), ce qui signifie qu’une grande partie des données n’appartient à aucune zone suffisamment dense selon les paramètres choisis.

Le cluster le plus important contient 78 points, tandis que les autres clusters sont beaucoup plus petits (10, 10, 9 et 6 points), ce qui montre que seules quelques régions du dataset présentent une densité suffisante pour être reconnues comme clusters.

Cette forte proportion de bruit suggère que le rayon eps=5 est probablement trop petit pour capturer la structure globale des données ou que les points sont très dispersés dans l’espace revenu/spending score.

En résumé, DBSCAN a détecté quelques groupes denses mais a considéré la majorité des clients comme isolés, ce qui reflète une segmentation très stricte basée sur la densité.