Du calcul à l’apprentissage: Feed Forward et Backpropagation

Feed forward: du signal d’entrée à la prédiction finale

Le feed forward (ou propagation avant) est le mécanisme fondamental qui permet à un réseau de neurones de produire une prédiction à partir de données d’entrée.

Concrètement, chaque neurone reçoit des valeurs en entrée, les pondère par ses poids, ajoute un biais, puis applique une fonction d’activation qui introduit de la non-linéarité. La sortie ainsi générée devient l’entrée de la couche suivante et ce processus se répète jusqu’à la couche finale.

À ce stade, le traitement dépend du type de tâche:

• En classification multi-classes: les valeurs brutes (appelées aussi logits) sont transformées en probabilités grâce à la fonction softmax (dont la formule est présentée plus bas), puis l’argmax sélectionne la classe ayant la probabilité la plus élevée.
• En classification binaire: on utilise généralement une sigmoid qui ramène la sortie à une probabilité entre 0 et 1, et la décision finale se fait par un seuil (souvent 0,5).
• En régression: il n’y a pas de transformation en probabilité car la sortie est une valeur numérique continue qui est directement interprétée comme la prédiction.

Formule de la fonction softmax:
\(z_i\): le logit (valeur brute) associé à la classe \(i\).
\(C\): le nombre total de classes.

Ce cheminement progressif transforme les données brutes en représentations de plus en plus abstraites, capables de capturer des relations complexes entre les variables. En pratique, le feed forward correspond donc au calcul direct de la sortie du réseau et constitue la première étape indispensable avant de mesurer l’erreur et d’entamer l’apprentissage par rétropropagation.

Calcul de l'erreur à l'aide de la fonction coût

Une fois la prédiction obtenue, elle est comparée à la valeur attendue (label) grâce à une fonction coût (ou loss function) qui mesure l’écart entre la sortie du réseau et la valeur réelle. Cette fonction fournit une valeur numérique appelée erreur, servant de signal d’apprentissage.

Dans les problèmes de régression, on utilise souvent l’erreur quadratique moyenne (MSE: Mean Squared Error), qui pénalise fortement les grandes différences, ou l’erreur absolue moyenne (MAE: Mean Absolute Error), plus robuste face aux valeurs extrêmes.

Je vous renvoie sur ma leçon sur la régression linéaire en Machine Learning où j'ai expliqué en détail (avec les formules mathématiques) chacune des fonctions coût possibles.

Pour les tâches de classification, la cross-entropy est privilégiée. La cross-entropy est une fonction coût qui mesure la distance entre deux distributions de probabilités: celle prédite par le réseau et celle attendue (les labels).

Concrètement, si le modèle attribue une forte probabilité à la mauvaise classe, la pénalité est élevée, ce qui pousse l’algorithme à corriger rapidement ses paramètres. Elle est particulièrement adaptée aux problèmes multi-classes car elle prend en compte toute la distribution des sorties et pas seulement la classe prédite.

On distingue souvent:

• Binary cross-entropy: La binary cross-entropy est une fonction coût utilisée lorsque la tâche de classification comporte deux classes (par exemple: "positif" vs "négatif", ou "spam" vs "non-spam"). Elle mesure la différence entre la probabilité prédite par le modèle et la valeur réelle (0 ou 1). A titre d'exemple, si la vraie classe est \(y=1\)et que le modèle prédit \(p=0.9\), la perte est faible car la prédiction est proche de la vérité. En revanche, si le modèle prédit p=0.1, la perte est élevée car il est très éloigné de la bonne classe.
• Categorical cross-entropy: La categorical cross-entropy est la fonction de coût la plus utilisée pour les tâches de classification multi-classes. Elle mesure la distance entre la distribution de probabilités prédite par le réseau et la distribution réelle des classes (souvent représentée par un one-hot vector).
  
  Formellement, pour une observation avec C classes, elle s’écrit:
  
  \(L=-\sum _{i=1}^Cy_i\cdot \log (p_i)\)
  \(y_i\) est la valeur réelle pour la classe \(i\) (1 pour la classe correcte, 0 pour les autres).
  \(p_i\) est la probabilité prédite par le modèle pour la classe \(i\).

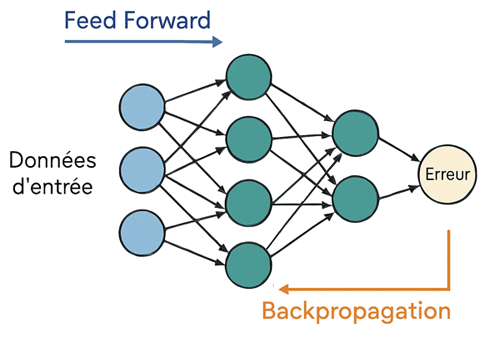
Backpropagation: propagation de l’erreur et optimisation des paramètres

Le backpropagation (ou rétropropagation) est l’algorithme central qui permet à un réseau de neurones d’apprendre à partir de ses erreurs.

Après le calcul de la prédiction et de l’erreur via la fonction coût, le réseau utilise les gradients (dérivées partielles de la fonction de coût par rapport aux poids et aux biais) pour savoir comment ajuster ses paramètres. Ces gradients indiquent à la fois la direction (augmenter ou diminuer un poids) et l’amplitude (de combien le modifier).

L’erreur est propagée en sens inverse, de la couche de sortie vers les couches cachées, afin de déterminer la contribution de chaque neurone à l’erreur finale. Ce mécanisme repose sur la règle de la chaîne de dérivation en calcul différentiel, qui permet de relier les variations locales de chaque neurone à l’impact global sur la fonction de coût.

Enfin, grâce à la descente de gradient, les poids et biais sont mis à jour à chaque itération, réduisant progressivement l’erreur. Répété sur des milliers d’exemples et plusieurs époques (epochs), ce processus permet au réseau de s’ajuster finement, de capturer des relations complexes et de généraliser sur de nouvelles données.

Optimisation moderne de la descente de gradient: Momentum, RMSProp et Adam

Outre la descente de gradient classique, plusieurs variantes ont été développées pour améliorer la vitesse et la stabilité de l’apprentissage des réseaux de neurones, en particulier, Mementum, RMSProp et Adam.

• Momentum: Le momentum introduit une mémoire des gradients passés afin de rendre l’optimisation plus fluide. Concrètement, il accumule une partie des mises à jour précédentes et les ajoute au gradient actuel, ce qui permet de lisser les oscillations et d’éviter les changements de direction trop brusques. Cette approche accélère la convergence vers le minimum en suivant une trajectoire plus stable particulièrement utile dans des paysages de fonction coût complexes où les gradients peuvent varier fortement d’une itération à l’autre.
• RMSProp: RMSProp (Root Mean Square Propagation) adapte dynamiquement le taux d’apprentissage pour chaque paramètre. Il calcule une moyenne mobile des carrés des gradients et utilise cette information pour normaliser les mises à jour. Ainsi, les poids associés à des gradients trop grands sont ralentis, tandis que ceux liés à des gradients plus faibles sont accélérés. Cette régulation évite que certains paramètres évoluent trop vite ou trop lentement, ce qui améliore la stabilité de l’entraînement, notamment sur des données hétérogènes ou bruitées.
• Adam: Adam (Adaptive Moment Estimation) combine les avantages du momentum et de RMSProp. Il tient compte à la fois de la moyenne des gradients (premier moment) et de leur variance (second moment), ce qui permet de produire des mises à jour plus robustes et efficaces. Adam ajuste automatiquement le taux d’apprentissage pour chaque paramètre tout en conservant une mémoire des directions passées, ce qui en fait un optimiseur particulièrement performant. Grâce à cette double prise en compte, il est devenu l’algorithme par défaut dans de nombreux cas pratiques car il assure une convergence rapide et stable même sur des problèmes complexes et des données bruitées.

Pour approfondir la compréhension de la descente de gradient, je vous invite à consulter la leçon dédiée à la démarche d’apprentissage en Machine Learning où ce mécanisme est expliqué plus en détail.