Classification supervisée multiclasse avec le dataset Iris

Prédiction des espèces florales à partir du jeu de données Iris

Nous allons appliquer une classification multiclasse sur le jeu de données Iris, qui est l’un des ensembles les plus connus en apprentissage automatique et que nous avons déjà manipulé de nombreuses fois. Ce dataset contient des mesures de fleurs appartenant à trois espèces différentes (setosa, versicolor et virginica).

L’objectif est de construire un modèle capable de prédire l’espèce d’une fleur à partir de ses caractéristiques (longueur et largeur des sépales et pétales). Pour cela, nous utiliserons un réseau de neurones avec une couche de sortie composée de trois neurones et une activation softmax, ce qui permet de produire une distribution de probabilités sur les trois classes. La fonction de perte adaptée est la categorical_crossentropy (ou sa variante sparse_categorical_crossentropy) si les labels ne sont pas encodés en one-hot) car elle est conçue pour les problèmes de classification multiclasse.

Encore une fois, je vous donnerai le code une seule fois et j'expliquera les points essentielles juste après.
On commence par appliquer une mise à l’échelle des variables X pour que chaque caractéristique soit ramenée dans un intervalle donné (par défaut entre 0 et 1).
Lorsqu’on utilise des réseaux de neurones, il est essentiel de normaliser les données d’entrée afin d’améliorer la stabilité et la rapidité de l’apprentissage. Cette étape est importante car les réseaux de neurones sont sensibles aux différences d’échelle entre les variables. En effet, une feature avec des valeurs très grandes peut dominer la fonction de coût et ralentir la convergence. En utilisant fit_transform sur l’ensemble d’entraînement (X_train), on calcule les bornes min/max uniquement sur ces données, puis on applique la même transformation à l’ensemble de test (X_test) avec transform, ce qui garantit la cohérence et évite toute fuite d’information.

On constuire notre réseaux de neurones (j'ai conservé le même nombre de couches et nombre de neurones que l'exemple de la séance précédente):
On utilise l’activation softmax en sortie car elle est spécialement conçue pour les problèmes de classification multiclasse. En effet, elle transforme les valeurs brutes du réseau en une distribution de probabilités qui somme à 1, ce qui permet d’associer chaque observation à la classe la plus probable parmi les trois espèces d’iris.

Ensuite, on compile notre modèle:
On utilise sparse_categorical_crossentropy quand les étiquettes des classes sont simplement des entiers (0, 1, 2 pour Iris) au lieu d’être transformées en vecteurs one‑hot. Cela permet d’entraîner directement le modèle sans étape supplémentaire de conversion des labels tout en obtenant les mêmes résultats qu’avec categorical_crossentropy appliqué sur des labels encodés.

L'étape suivante consiste à produire les prédictions et illustrer les performances de la classification:
On utilise argmax dans ce cas car la sortie du modèle est une matrice de probabilités produite par la fonction softmax. En effet, chaque ligne correspond à un échantillon et contient une probabilité pour chacune des classes (par exemple [0.1, 0.7, 0.2]). Pour transformer ces probabilités en prédictions de classes, il faut choisir la classe ayant la probabilité la plus élevée. C’est exactement ce que fait argmax(axis=1) qui il renvoie l’indice de la probabilité maximale sur chaque ligne, donc la classe prédite (0, 1 ou 2 pour Iris).

La dernière étape consiste à illustrer la learning curve:
Ce qui produit ce graphique:

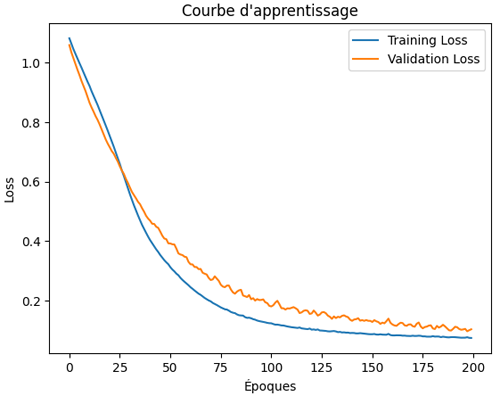
On constate dans cette courbe d’apprentissage que la loss et la val_loss continuent à descendre, ce qui indique que le modèle n’a pas encore atteint son point de stabilisation. Cela signifie qu’il apprend encore et qu’il n’est pas en situation d'overfitting.

Dans ce cas, prolonger l’entraînement en ajoutant davantage d’époques pourrait permettre d’améliorer la performance du modèle, car il continuerait à réduire l’erreur et à mieux s’adapter aux données.