De la régression linéaire à la régression non linéaire

Apprendre à modéliser une relation quadratique avec Keras

Dans cette nouvelle étape, nous allons aborder un problème de régression non linéaire en construisant un modèle capable de capturer une relation quadratique entre les données artificielles générées et leur cible.

Concrètement, nous allons créer un jeu de données où la variable explicative X est reliée à la sortie y par une fonction polynomiale de degré 2, enrichie éventuellement d’un bruit aléatoire pour simuler des observations réalistes.

Le réseau de neurones sera conçu avec Keras en utilisant une architecture Sequential, composée de plusieurs couches Dense afin de permettre au modèle d’apprendre cette courbure non linéaire.

Code intégral et ajustements par rapport à la version précédente

L’objectif est de montrer comment un réseau de neurones peut dépasser les limites d’une simple régression linéaire et s’adapter à des structures de données plus riches.

Cette fois, je vais vous présenter le code dans son intégralité afin que vous puissiez le parcourir et l’exécuter tel quel. Une fois le programme exposé, nous analyserons ensemble les différentes étapes et je mettrai en évidence les modifications que nous avons apportées par rapport au code de la dernière séance.

L’objectif est de vous montrer concrètement comment l’architecture évolue pour traiter un problème non linéaire et de clarifier les choix techniques qui rendent le modèle plus adapté à une relation quadratique. Vous aurez ainsi une vision complète du script avant de plonger dans les explications détaillées.

Scaling des variables

Le scaling est une étape essentielle avant l’entraînement d’un réseau de neurones car les variables d’entrée peuvent avoir des échelles très différentes. Sans normalisation, les poids du modèle doivent compenser ces écarts, ce qui ralentit la convergence et peut rendre l’optimisation instable.

L’outil MinMaxScaler de scikit-learn permet de transformer chaque feature en la ramenant dans un intervalle défini, généralement [0,1]. Ainsi, toutes les données sont mises sur un pied d’égalité, ce qui facilite le travail de l’optimiseur (comme Adam) et améliore la précision de l’apprentissage.

En pratique, cela garantit que le réseau de neurones se concentre sur la structure des relations entre les variables plutôt que sur leurs différences d’échelle.

Construction du modèle avec Keras

Dans ce modèle, nous avons choisi d’ajouter deux couches cachées de type Dense avec 50 neurones chacune et une activation ReLU. L’idée est que chaque couche cachée permet au réseau de construire des représentations plus complexes des données: la première couche extrait des motifs non linéaires de base, tandis que la seconde affine ces représentations pour mieux capturer la relation quadratique entre X et y. En pratique, multiplier les couches cachées augmente la capacité du réseau à modéliser des fonctions plus riches et à s’adapter à des données qui ne suivent pas une simple relation linéaire.

Compilation du modèle et aperçu de sa structure

A chaque fois que l’on ajoute une couche cachée dans un réseau de neurones, le nombre de paramètres à apprendre (poids et biais) augmente très rapidement. Cela peut rendre le modèle plus puissant, mais aussi plus coûteux en calcul et plus susceptible de surapprendre si les données sont limitées.

Entrainement du modèle

Nous avons augmenté le nombre d’époques à 300 (contre 100 de l'exemple précédent) pour donner au modèle davantage de temps d’apprentissage. En effet, lorsqu’on traite un problème non linéaire, la fonction à approximer est plus complexe qu’une simple droite et le réseau a besoin de plusieurs passages sur les données pour ajuster correctement ses poids.

Avec trop peu d’époques, le modèle risque de ne pas converger et de rester bloqué dans une approximation grossière. En allongeant l’entraînement, on permet à l’optimiseur (ici Adam) de réduire progressivement l’erreur et de capturer la forme quadratique de la relation.

Affichage des graphiques (valeurs réelles vs valeurs prédites)

Après l’entraînement, les prédictions du modèle sont exprimées dans l’échelle normalisée utilisée par le MinMaxScaler. Or, ces valeurs ne correspondent pas directement aux données originales, ce qui rend leur interprétation et leur visualisation difficiles. C’est pourquoi nous effectuons une remise à l’échelle inverse (inverse_transform) aussi bien pour les entrées X, les sorties réelles y, que pour les prédictions y_pred.

Cette étape permet de retrouver les unités et les amplitudes initiales des données afin de comparer correctement les valeurs prédites aux valeurs réelles et de tracer des graphiques lisibles et cohérents.

Après exécution, nous obtenons ce graphique:

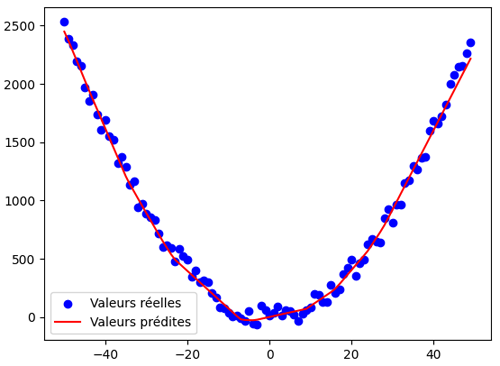
On constate que les valeurs prédites par le réseau de neurones épousent parfaitement la forme quadratique des données réelles. Cette performance est particulièrement intéressante car elle est atteinte sans avoir recours au feature engineering classique, comme la création manuelle de polynomial features utilisée en Machine Learning traditionnel. Autrement dit, le réseau de neurones parvient à apprendre directement la courbure des données grâce à ses couches cachées et à ses fonctions d’activation, ce qui illustre sa capacité à modéliser des relations complexes de manière automatique et élégante.