Polynomial Features: enrichir les données pour capturer la non‑linéarité

Preprocessing vs Feature Engineering - Rappel

Dans les leçons précédentes, nous avons vu que le preprocessing est l’ensemble des étapes qui permettent de préparer les données avant de les donner à un modèle. L’objectif est de rendre les données propres, cohérentes et exploitables. Cela inclut par exemple la gestion des données manquantes, le nettoyage (supprimer les doublons ou corriger des erreurs), l’imputation (remplir les trous dans les données), le scaling ou encore le label encoding et le One-Hot Encoding (transformer des variables catégorielles comme "rouge, vert, bleu" en chiffres que le modèle peut comprendre). Ces opérations ne changent pas la nature des variables mais les rendent simplement utilisables.

Le feature engineering en revanche, va plus loin. En effet, il s’agit de créer de nouvelles caractéristiques ou de transformer celles qui existent pour aider le modèle à mieux apprendre. Par exemple, si l’on a une variable "âge", on peut créer une nouvelle variable "âge²" pour capturer une relation non linéaire. On peut aussi combiner deux variables (par exemple "taille × poids") pour révéler une interaction etc...

Les Polynomial Features sont un bon exemple de feature engineering, car à partir d’une variable simple, on génère ses puissances et ses combinaisons afin d’enrichir l’espace des données.

En quoi consiste les Polynomial Features?

Les Polynomial Features permettent de transformer des variables simples en un espace plus riche pour capturer des relations non linéaires. Si l’on prend une seule variable \(x\), au lieu de n’avoir que \(x\), on peut générer \(x^2\),\(x^3\)... ce qui permet à un modèle linéaire de s’adapter à une courbe quadratique ou cubique.

Par exemple, avec \(x=3\), on obtient \([3,9,27]\). Si l’on considère maintenant deux variables \(x_1\) et \(x_2\), les Polynomial Features de degré 2 produisent : \([x_1,x_2,x_1^2,x_2^2,x_1\cdot x_2]\). Ainsi, pour (\(x_1=2\),\(x_2=3\)), on obtient \([2,3,4,9,6]\). Cette expansion enrichit le jeu de données en ajoutant des puissances et des interactions, ce qui permet aux modèles linéaires de représenter des relations plus complexes entre les variables.

Application des Polynomial Features dans un environnement Python

L’objectif de ce travail est d’illustrer la mise en place d’un modèle capable de traiter des données dont la relation entre les variables n’est pas linéaire. En effet, l’ensemble considéré est construit à partir d’une variable explicative X allant de -100 à 100 et d’une variable cible y définie comme le carré de X auquel s’ajoute un bruit aléatoire. Cette construction génère une courbe en forme de parabole perturbée, ce qui rend inadaptée une simple régression linéaire. L’intérêt est donc de montrer comment des techniques comme l’extension polynomiale des caractéristiques permettent de capturer cette structure non linéaire et d’améliorer la qualité de la modélisation.

Dans ce cadre, nous présenterons deux implémentations distinctes : la première sans recours aux Polynomial Features et la seconde en les intégrant afin de mettre en évidence la différence de performance et la capacité du modèle à capturer la nature non linéaire des données.

Régressin linaire sans Polynomal Features

Je propose le code suivant:
Après exécution du code on obtient le score de détérminiation suivant:
Cela indique que le modèle linéaire simple (sans Polynomial Features) ne parvient pas du tout à expliquer la relation entre X et y.

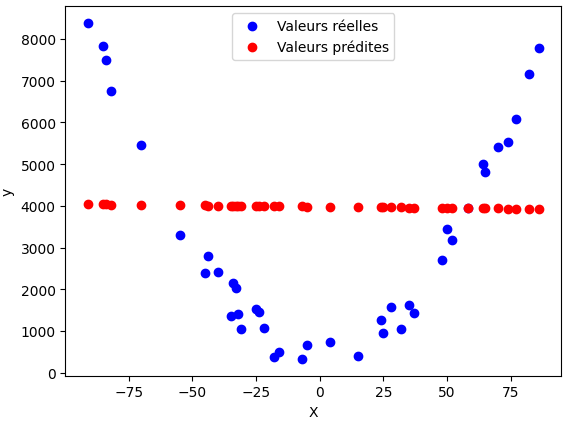
En observant le graphique, on voit que les points rouges des prédictions s’éloignent fortement des points bleus des valeurs réelles, ce qui montre que l’erreur est très grande, car le modèle tente d’ajuster une droite alors que les données suivent une forme quadratique.

Régressin linaire avec Polynomal Features

Cette fois je propose ce code:
Expliquons rapidement les points importants de ce code:

On commence par importer les modules nécessaires, dont bPolynomialFeatures de scikit-learn:
Ensuite, on initialise un générateur de features polynomiales de degré 2:
Le paramètre include_bias=False indique qu’on ne veut pas ajouter la colonne de constantes (1), puisque le modèle de régression gère déjà son propre biais (intercept). En effet, scikit-learn ajoute une colonne de 1 par défaut (include_bias=True) et qui correspond au terme constant (biais) du modèle.

Dans le même code, on transforme les données d’entraînement et de test en ajoutant les nouvelles variables polynomiales générées par PolynomialFeatures.

Cette fois on on obient cette valeur en guise de coefficient de détermination:
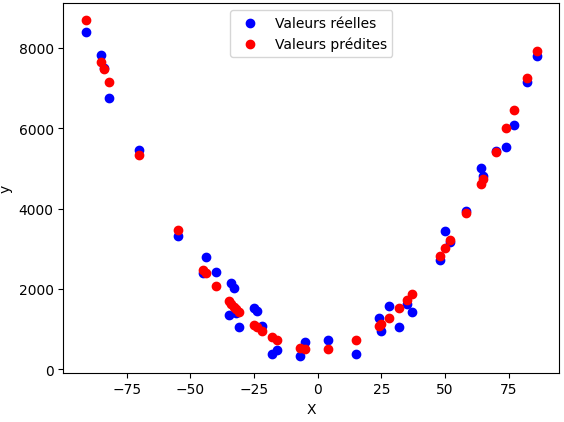
Cela signifie que le modèle explique près de 98,5% de la variance des données. Autrement dit, les prédictions sont très proches des valeurs réelles et l’ajustement est excellent. D'ailleurs, en regardant le graphique, on remarque que les points prédits reproduisent fidèlement la forme en parabole des données observées:

Verdict final

Là où la régression linéaire simple échouait (score négatif), l’extension polynomiale transforme le problème en un modèle adapté capable de suivre presque parfaitement la courbe réelle. En résumé, l’ajout des Polynomial Features rend le modèle pertinent et performant pour des données non linéaires.