Le neurone artificiel: l’unité de base d'un réseau de neurones

Qu'est ce qu'un neurone artificiel?

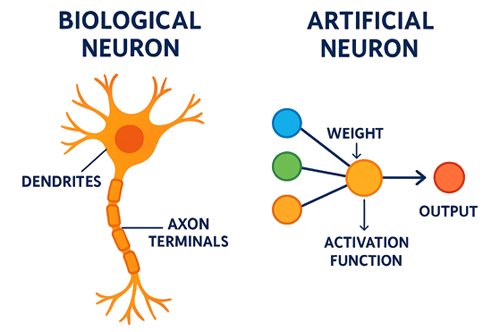
Le neurone artificiel est directement inspiré du fonctionnement du neurone biologique. Dans le cerveau, un neurone reçoit des signaux électriques par ses dendrites, les intègre dans son corps cellulaire, puis décide de déclencher ou non une impulsion nerveuse. Cette impulsion, appelée potentiel d’action, circule le long de l’axone jusqu’aux synapses où elle peut activer d’autres neurones. Ce mécanisme biologique illustre une logique simple mais puissante: réception, traitement et transmission de l’information.

De manière analogue, le neurone artificiel reprend cette logique sous une forme mathématique simplifiée. Il reçoit des valeurs numériques en entrée, leur attribue des poids qui traduisent leur importance, ajoute un biais pour ajuster la flexibilité du modèle, puis calcule une somme pondérée. Cette somme est ensuite transformée par une fonction d’activation, qui détermine la sortie du neurone. La valeur produite est transmise aux autres neurones du réseau, permettant ainsi à l’ensemble du système d’apprendre et de construire des représentations de plus en plus complexes.

Les entrées et les poids d'un neurone

Chaque neurone artificiel reçoit des entrées qui représentent directement les données du problème à traiter. Ces entrées peuvent être très variées:

• Les pixels d’une image, qui traduisent l’intensité lumineuse de chaque point, et parfois même ses nuances de couleur.
• Les mots d’un texte transformés en vecteurs numériques grâce à des techniques comme l’encodage, l'extraction de caractéristiques ou l’embedding.
• Les caractéristiques et attributs d’un client, comme son âge, son revenu ou son historique d’achats.

À chaque entrée (notée \(x_i\)) est associé un poids (noté \(w_i\)). Ce poids joue le rôle d’un coefficient qui indique à quel point l’entrée est déterminante pour la sortie du neurone. Par conséquent, un poids élevé signifie que l’information est jugée très importante et influence fortement le calcul. A l'inverse, un poids faible ou nul indique que l’information a peu d’impact, voire aucun.

Ainsi, le neurone ne traite pas toutes les données de manière uniforme mais il hiérarchise leur importance et apprend à donner plus de valeur aux signaux pertinents.

Le blais: pour ajuster la flexibilité

En plus des poids, chaque neurone possède un biais \(b\) qui permet de décaler la fonction d’activation et d’ajuster la flexibilité du modèle. Sans biais, le neurone serait limité dans sa capacité à représenter certaines relations. C’est un paramètre crucial qui améliore la précision et la capacité d’adaptation du réseau.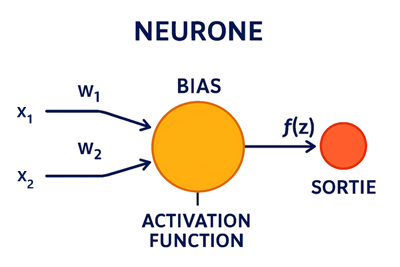

Le neurone calcule une somme pondérée des entrées et du biais:
Cette valeur \(z\) est une combinaison linéaire des données. Mais à ce stade, le neurone reste une simple fonction linéaire incapable de capturer des relations complexes.

La fonction d’activation: introduire la non-linéarité

Sans fonction d’activation, un réseau de neurones ne serait qu’une simple combinaison linéaire incapable de modéliser des relations complexes.

La fonction d’activation introduit une non-linéarité, ce qui permet au réseau de:

• Capturer des motifs complexes dans les données. En effet, la fonction d’activation est ce qui permet au réseau de neurones de modéliser des relations non linéaires. Sans elle, chaque neurone ne ferait qu’une combinaison linéaire des entrées, ce qui limiterait drastiquement la capacité du réseau à apprendre des structures complexes.
  
• Décider si un neurone "s’active" ou non. Dans ce cas, la fonction d’activation agit comme un filtre décisionnel. Elle permet au neurone de choisir s’il doit transmettre ou non son signal à la couche suivante.
  
• Contrôler la propagation des signaux. Là encore, la fonction d’activation joue un rôle crucial dans la régulation du flux d’information à travers le réseau. Elle permet d’éviter que les valeurs explosent ou s’annulent (problèmes de gradient), de normaliser les sorties pour qu’elles restent dans des plages gérables et de faciliter l’apprentissage en limitant les effets extrêmes.

C’est grâce à la fonction d'activation que les réseaux de neurones peuvent apprendre à reconnaître des images, comprendre du texte ou prédire des comportements complexes.

Types de fonctions d'activation

Il existe plusieurs fonctions d’activation, chacune adaptée à un contexte particulier:

• Sigmoïde: La fonction sigmoïde transforme toute valeur en une sortie comprise entre 0 et 1. Elle est particulièrement utile lorsqu’on veut modéliser une probabilité, par exemple pour répondre à une question du type: "Est-ce que cette image contient un chat, oui ou non?" (Fonction 1).
• Tanh: La tangente hyperbolique (tanh) produit des sorties entre -1 et 1, ce qui permet au réseau de travailler avec des valeurs centrées autour de zéro. Cela facilite l’apprentissage car les gradients sont mieux répartis et les mises à jour des poids sont plus stables (Fonction 2).
• ReLU: La fonction ReLU (Rectified Linear Unit) est devenue la norme dans les réseaux profonds. Elle est très simple: si l’entrée est négative, la sortie est zéro, sinon, la sortie est égale à l’entrée (Fonction 3).
• Softmax: La fonction Softmax est utilisée en sortie des réseaux de classification multiclasses. Elle prend un vecteur de valeurs (par exemple, les scores pour chaque classe) et le transforme en probabilités normalisées dont la somme est égale à 1 (Fonction 4).
• Fonction linéaire: La fonction linéaire ne transforme pas la valeur d’entrée: elle la transmet telle quelle. Elle est utilisée lorsque la sortie attendue est une valeur continue (problème de régression), comme le prix d’un bien immobilier, la température prévue demain ou le score d’un utilisateur (Fonction 5).

Organisation et interconnexion des neurones dans un réseau

Les neurones ne fonctionnent pas isolément mais ils sont organisés en couches. Les couches sont réarties en trois types: la couche d'entrée, la (ou les) couche(s) cachée(s) et la couche de sortie.

• La couche d’entrée: La couche d’entrée est la porte d’entrée du réseau. Elle reçoit directement les données brutes issues du problème à résoudre. Par exemple, dans une image, chaque pixel peut être une entrée et dans un tableau de données, chaque caractéristique (âge, revenu, nombre d’enfants…) est une entrée. Cette couche ne transforme pas les données mais elle se contente de les transmettre aux neurones de la couche suivante.
• Les couches cachées: Les couches cachées sont les zones de calcul où les données sont progressivement transformées. Chaque neurone de ces couches applique des poids aux entrées qu’il reçoit, ajoute un biais, puis utilise une fonction d’activation pour produire une sortie. C’est dans ces couches que le réseau apprend à extraire des motifs et des représentations complexes des données.
• La couche de sortie: La couche de sortie est la conclusion du réseau. Elle prend les informations produites par les couches cachées et les traduit en un résultat exploitable. En effet, dans une tâche de classification, elle peut donner une probabilité pour chaque classe (par exemple: chat, chien, oiseau...) et dans une tâche de régression, elle peut fournir une valeur numérique (par exemple: le prix estimé d’une maison).

Les différents types de connexions entre neurones

Architecture fully connected (dense)

Dans une architecture dite "fully connected" (ou dense), chaque neurone d’une couche est relié à l’ensemble des neurones de la couche suivante. Ce maillage complet assure une circulation totale de l’information, permettant au réseau de combiner toutes les données disponibles et de produire des représentations complexes et riches.

Cette organisation dense constitue le modèle de base largement adopté dans les réseaux classiques tels que les Multi-Layer Perceptrons, où cette connectivité favorise une forte capacité d’apprentissage et une grande flexibilité dans le traitement des données.

Connexions convolutionnelles (CNN)

Dans les réseaux de neurones convolutionnels (CNN), les neurones ne sont pas reliés à toute la couche suivante comme dans une architecture fully connected. Au contraire, chaque neurone est connecté uniquement à une petite région locale des données, appelée réceptif local. Par exemple, lorsqu’on analyse une image, un neurone peut se concentrer sur un petit patch de pixels (une zone de quelques points) plutôt que sur l’image entière.

Cette approche locale permet au réseau de détecter des motifs visuels élémentaires tels que des bords, des textures ou des formes simples. En combinant plusieurs couches convolutionnelles, le réseau parvient à reconnaître des structures de plus en plus complexes: d’abord des lignes et des angles, puis des objets entiers comme des visages ou des lettres.

Connexions récurrentes (RNN)

Dans les réseaux récurrents, les neurones ne se contentent pas d’envoyer leur sortie à la couche suivante mais ils sont également reliés à eux‑mêmes ou aux couches précédentes. Cette particularité crée une mémoire interne qui permet au réseau de conserver une trace des informations déjà traitées. Contrairement aux architectures classiques où chaque entrée est analysée indépendamment, les RNN prennent en compte le contexte passé pour influencer le calcul actuel.

Ce mécanisme est particulièrement adapté aux données séquentielles, comme le texte, l’audio ou les séries temporelles. Par exemple, lorsqu’on lit une phrase, le sens d’un mot dépend souvent de ceux qui le précèdent. Grâce aux connexions récurrentes, le réseau peut prédire le mot suivant en tenant compte de l’ensemble de la séquence déjà parcourue. De la même manière, dans une série temporelle, il peut anticiper une valeur future en s’appuyant sur l’évolution des valeurs passées.

Connexions résiduelles (ResNet)

Dans les réseaux résiduels, l’innovation majeure réside dans l’introduction de connexions directes entre des couches non consécutives. Ces connexions appelées skip connections ou raccourcis, permettent de transmettre l’information brute d’une couche à une autre sans passer par toutes les transformations intermédiaires. Autrement dit, le réseau peut comparer la sortie transformée avec l’entrée initiale et apprendre plus facilement à ajuster ses calculs.

Ce mécanisme est particulièrement utile dans les réseaux très profonds où l’accumulation de transformations peut entraîner une perte d’information et un affaiblissement du signal lors de la rétropropagation. Les connexions résiduelles facilitent la circulation du gradient à travers les couches, ce qui aide à résoudre le problème du gradient qui disparaît et permet d’entraîner des architectures beaucoup plus profondes avec efficacité. Grâce à cette approche, les ResNet ont marqué une avancée majeure en vision par ordinateur en permettant de construire des modèles performants tout en restant stables à l’entraînement.

Connexions par attention (Transformers)

Dans les architectures modernes comme les Transformers, les neurones ne suivent plus une logique de connexions fixes entre couches successives. Au contraire, ils peuvent se connecter de manière sélective à d’autres neurones en fonction de la pertinence de l’information. Cette flexibilité permet au modèle de ne pas traiter toutes les données de la même façon, mais de mettre l’accent sur les éléments réellement significatifs.

Le cœur de cette approche est le mécanisme d’attention. Celui-ci attribue des poids variables aux connexions, afin de déterminer quelles parties des données méritent le plus d’attention. Par exemple, dans une phrase, certains mots influencent fortement le sens global, tandis que d’autres sont secondaires. L’attention permet au modèle de se concentrer sur ces mots clés, de relier des éléments éloignés dans la séquence et de construire une compréhension plus fine.

C’est grâce à ce principe que les Transformers sont devenus incontournables dans le traitement du langage naturel (traduction, résumé, génération de texte) et dans l’analyse de séquences complexes comme l’audio ou même certaines données visuelles. Ils offrent une capacité unique à capturer le contexte global tout en hiérarchisant l’importance des informations.

En résumé, un réseau de neurones n’est pas limité à l’architecture fully connected. Selon la tâche, il peut utiliser des connexions locales (CNN), séquentielles (RNN), résiduelles (ResNet) ou sélectives (attention). Chaque type de connexion apporte une manière différente de propager et transformer l’information, ce qui rend les réseaux adaptés à une grande variété de problèmes.