Recurrent Neural Networks (RNN): Comprendre et modéliser les dépendances séquentielles

Pourquoi les réseaux de neurones recurrents RNN?

Après les réseaux de neurones convolutifs (CNN) qui excellent dans l’analyse d’images et de données spatiales, un autre défi majeur apparaît, c'est celui des données séquentielles.

Les textes, les séries temporelles, les signaux audio ou encore les données financières ne se présentent pas comme des images fixes, mais comme des suites ordonnées où chaque élément dépend du précédent. Les réseaux de neurones classiques ou mêmes les CNN ne sont pas conçus pour capturer cette dépendance temporelle. En effet, ces architectures traitent chaque entrée comme indépendante, ce qui limite leur capacité à comprendre le contexte ou la continuité. C’est précisément pour répondre à ce problème qu’ont été introduits les RNN, capables de modéliser la dynamique des séquences.

Qu'est ce qu'un réseaux de neurones cocurrents?

Un RNN (Recurrent Neural Network) est une architecture de réseau de neurones conçue pour traiter des données séquentielles en intégrant une notion de mémoire.

Contrairement aux réseaux classiques, un RNN réutilise ses sorties internes comme entrées pour l’étape suivante, créant ainsi une boucle récurrente. Cette structure lui permet de conserver une trace des états passés et de prendre en compte le contexte dans ses prédictions. En d’autres termes, les RNN ne se contentent pas d’analyser un élément isolé, mais cherchent à comprendre la relation entre les éléments successifs d’une séquence, ce qui les rend particulièrement adaptés au traitement du langage naturel, à la reconnaissance vocale ou à la prévision de séries temporelles.

Vue folded et unfolded d'un RNN

On peut représenter un réseau de neurones récurrent (RNN) de deux façons complémentaires:

• Forme folded: où l’on visualise un seul bloc récurrent avec sa boucle interne qui illustre la mémoire du réseau.
• Forme unfolded: où ce même bloc est déployé dans le temps pour montrer la succession des étapes et la propagation de l’état caché d’une entrée à l’autre.

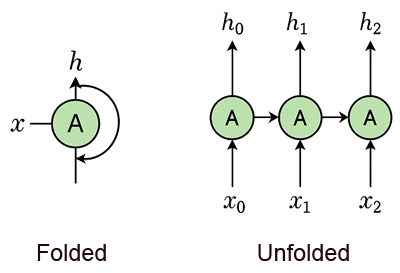
Dans sa forme compacte (folded), le RNN est représenté par un seul bloc récurrent qui reçoit une entrée \(x\) et produit une sortie \(h\). Ce bloc est doté d’une boucle interne: une flèche relie sa sortie à sa propre entrée, illustrant la capacité du réseau à mémoriser l’information précédente. Cette structure repliée permet de visualiser le principe fondamental du RNN, c'est à dire qu'à chaque instant, il traite une donnée tout en tenant compte de son état antérieur, ce qui le rend apte à modéliser des séquences.

Lorsqu’on déplie le RNN dans le temps (unfolded), on obtient une série de blocs identiques connectés les uns aux autres. Chaque bloc reçoit une entrée spécifique à son instant \(x_0\), \(x_1\), \(x_2\) et produit une sortie correspondante \(h_0\), \(h_1\), \(h_2\). Les flèches entre les blocs montrent la propagation de l’état caché d’un pas de temps au suivant. Cette vue unfolded révèle que le RNN est en réalité une chaîne dynamique où chaque étape dépend des précédentes, permettant ainsi de capturer les dépendances temporelles dans les données séquentielles comme le texte, l’audio ou les séries chronologiques.

L’état caché dans un RNN

Dans un réseau de neurones récurrent (RNN), l’état caché est la composante essentielle qui permet au modèle de conserver une mémoire des informations passées. À chaque pas de temps, le RNN reçoit une nouvelle entrée \(x_t\) et combine celle-ci avec l’état caché précédent \(h_{t-1}\) pour produire un nouvel état \(h_t\). Cet état caché agit comme une mémoire dynamique, stockant le contexte accumulé au fil de la séquence et influençant les prédictions futures.

En d’autres termes, un RNN ne se limite pas à traiter l’entrée courante, mais intègre également l’historique, ce qui rend cette architecture capable de modéliser des dépendances temporelles et de comprendre la continuité dans des données séquentielles comme le langage, la musique ou les séries chronologiques.

Dans un réseau de neurones récurrent, l’état caché est mis à jour à chaque pas de temps (time step) par une fonction qui combine l’entrée courante et l’état précédent. Mathématiquement, cette mise à jour s’écrit généralement :

• \(x_t\): l’entrée au temps t qui correspond simplement à la donnée reçue par le réseau à un instant précis de la séquence.
• \(h_{t-1}\): l’état caché du pas précédent. Il correspond à la représentation interne qui résume les informations déjà traitées dans la séquence et qui sera combinée avec l’entrée courante pour produire le nouvel état caché \(h_t\).
  
• \(W\) et \(U\): matrices de poids associées respectivement à l’entrée et à l’état caché. Il s'agit des paramètres du réseau à entraîner (en plus du biais). Autrement dit, ce sont eux qui s’ajustent durant l’apprentissage afin que le RNN apprenne à modéliser correctement les dépendances dans les données séquentielles.
• \(b\): biais qui est un paramètre supplémentaire ajouté à la combinaison linéaire des entrées et des poids, permettant au modèle de décaler la fonction d’activation et d’améliorer sa capacité d’adaptation aux données.
• \(f\): fonction d’activation, souvent choisie parmi des options comme tanh ou ReLU. Il s'agit du mécanisme qui introduit de la non-linéarité dans le calcul du RNN et permet au réseau de modéliser des relations complexes dans les données séquentielles.

Cette équation illustre que l’état caché \(h_t\) est une mémoire dynamique, intégrant à la fois l’information nouvelle et le contexte accumulé. Ainsi, le RNN peut capturer les dépendances temporelles dans une séquence, ce qui le rend adapté au traitement du langage, des séries chronologiques ou des signaux audio.

Domaines d'application des RNN

Les RNN sont largement utilisé dans de nombreux domaines. Leurs principales applications sont:

• Traitement du langage naturel (NLP): les RNN sont utilisés pour la traduction automatique, la génération de texte ou encore l’analyse de sentiments, car ils savent prendre en compte le contexte des mots dans une phrase.
• Reconnaissance vocale:
• : ils permettent de convertir la parole en texte en tenant compte de la continuité des sons, ce qui améliore la précision par rapport à des modèles qui traiteraient chaque son isolément.
• Prédiction de séries temporelles: dans la finance, la météo ou l’énergie, les RNN exploitent les données passées pour anticiper les valeurs futures en capturant les tendances et les dépendances temporelles.
• Analyse de séquences biologiques: ils servent à modéliser des séquences d’ADN ou de protéines où l’ordre des éléments est crucial pour comprendre la structure et la fonction.
• Musique et audio: les RNN peuvent générer des mélodies cohérentes ou classer des sons, en tenant compte de la progression temporelle des notes ou des signaux.
• Vision par ordinateur séquentielle: dans des tâches comme la description d’images (image captioning) ou l’analyse de vidéos, les RNN permettent de relier les informations visuelles à une séquence linguistique ou temporelle.

Limites des RNN et améliorations avec LSTM et GRU

Bien que les réseaux de neurones récurrents (RNN) soient puissants pour traiter des séquences, ils présentent plusieurs limites. En particulier, ils souffrent du problème du gradient qui disparaît (vanishing gradient) ou explose (exploding gradient) lors de l’entraînement sur de longues séquences, ce qui les rend incapables de capturer efficacement des dépendances à long terme. De plus, leur mémoire est relativement courte et leur apprentissage peut devenir instable ou inefficace.

Pour surmonter ces difficultés, des variantes améliorées ont été introduites, en l'occurrence les LSTM (Long Short-Term Memory) et les GRU (Gated Recurrent Unit). Ces architectures intègrent des mécanismes de portes qui régulent le flux d’information, permettant de conserver ou d’oublier certaines données de manière sélective.