Deep Learning: comprendre et construire des réseaux de neurones






Leçon 13: CNN et MNIST: reconnaissance et classification des chiffres manuscrits
Toutes les leçons 

Deep Learning: comprendre et construire des réseaux de neurones
Leçon 13
CNN et MNIST: reconnaissance et classification des chiffres manuscrits
CNN et MNIST: reconnaissance et classification des chiffres manuscrits
Reconnaître les chiffres manuscrits du dataset MNIST avec les CNN
Le dataset MNIST de reconnaissance de chiffres manuscrits
Le dataset MNIST (Modified National Institute of Standards and Technology) est l’un des ensembles de données les plus célèbres en apprentissage automatique. Il contient 70 000 images de chiffres manuscrits (60 000 pour l’entraînement et 10 000 pour le test), chacune étant une image en niveaux de gris de 28×28 pixels représentant un chiffre entre 0 et 9.Le dataset MNIST a été popularisé par Yann LeCun, pionnier du deep learning et titulaire du prix Turing 2018 (souvent considéré comme le "prix Nobel de l’informatique"), en reconnaissance de ses travaux fondateurs sur les réseaux de neurones convolutionnels (CNN).
MNIST est devenu un standard pédagogique car il est simple, rapide à manipuler et permet d’obtenir des performances très élevées avec des architectures relativement modestes.
On peut trouver le dataset MNIST :
- Sur le site officiel de Yann LeCun (l’un des créateurs du dataset): http://yann.lecun.com.
- Directement intégré dans TensorFlow/Keras via tf.keras.datasets.mnist, ce qui permet de le charger en une seule ligne de code.
Le dataset MNIST existe aussi dans une variante appelée Fashion-MNIST qui contient des images de vêtements (t-shirts, pantalons, chaussures, sacs...) au lieu de chiffres manuscrits. Comme MNIST, il propose des images en niveaux de gris de 28×28 pixels, mais avec des classes plus complexes et visuellement proches les unes des autres.
Mise en place d'une architecture CNN pour la reconnaissance des chiffres manuscrits
Note objectif consiste à construire un réseau de neurones convolutionnel capable d’extraire automatiquement les caractéristiques visuelles des images du dataset MNIST. Chaque image (28×28 pixels en niveaux de gris) est d’abord normalisée puis transmise à des couches de convolution qui détectent des motifs simples (traits, courbes), suivies de couches de pooling qui réduisent la dimension tout en conservant l’essentiel de l’information. Ces représentations hiérarchiques sont ensuite aplaties et envoyées vers des couches entièrement connectées qui réalisent la classification finale en attribuant une probabilité à chacun des dix chiffres (0–9).On commence par l'importation des modules nécessaires:
import tensorflow as tf
from tensorflow.keras import datasets, layers, models
import matplotlib.pyplot as plt
import numpy as np
Ensuite, on charge le dataset MNIST:
from tensorflow.keras import datasets, layers, models
import matplotlib.pyplot as plt
import numpy as np
(X_train, y_train), (X_test, y_test) = datasets.mnist.load_data()
La fonction load_data() renvoie deux ensembles distincts sous forme de tuples: le premier contient les données et les labels d’entraînement (60 000 exemples), et le second contient les données et les labels de test (10 000 exemples).
La prochaine opération consiste au reshape et à la normalisation des images:
X_train = X_train
.reshape(-1, 28, 28, 1)
.astype("float32") / 255.0
X_test = X_test
.reshape(-1, 28, 28, 1)
.astype("float32") / 255.0
.reshape(-1, 28, 28, 1)
.astype("float32") / 255.0
X_test = X_test
.reshape(-1, 28, 28, 1)
.astype("float32") / 255.0
- Reshape: les images, initialement stockées sous forme de matrices 2D (28×28), sont transformées en tenseurs 4D de la forme (nombre_d’images, hauteur, largeur, canaux). Ici, -1 laisse Python calculer automatiquement le nombre d’images et 1 indique qu’il s’agit d’images en niveaux de gris (un seul canal).
- Normalisation: la conversion en float32 puis la division par 255.0 ramènent les valeurs des pixels (initialement entre 0 et 255) dans l’intervalle [0,1]. Cela facilite l’apprentissage du réseau en évitant des valeurs trop grandes et en accélérant la convergence.
Ensuite, on réalise l’encodage one-hot des labels.
y_train_cat = tf.keras.utils.to_categorical(y_train, 10)
y_test_cat = tf.keras.utils.to_categorical(y_test, 10)
Dans MNIST, les labels sont des entiers allant de 0 à 9 (par exemple, 3 pour le chiffre "3"). Or, un réseau de neurones fonctionne mieux lorsque les classes sont représentées sous forme de vecteurs binaires où chaque position correspond à une classe possible. Par exemple: le chiffre 3 devient le vecteur [0, 0, 0, 1, 0, 0, 0, 0, 0, 0].
y_test_cat = tf.keras.utils.to_categorical(y_test, 10)
Donc, la méthode to_categorical transforme automatiquement les labels en vecteurs de taille 10, ce qui permet au modèle CNN de produire une sortie sous forme de probabilités pour chacune des 10 classes puis de choisir la plus élevée comme prédiction finale.
On affiche 5 images du dataset MNIST au début de l’exécution afin de donner un aperçu concret des données manipulées:
plt.figure(figsize=(10, 2))
for i in range(5):
plt.subplot(1, 5, i+1)
plt.imshow(X_train[i].reshape(28,28), cmap="gray")
plt.title(f"Label: {y_train[i]}")
plt.axis("off")
plt.show()
L'instruction plt.subplot(1, 5, i+1) indique à Matplotlib de créer une figure composée de 1 ligne et 5 colonnes de sous‑graphiques, puis de placer l’image courante dans la position i+1 (de la première à la cinquième case).
for i in range(5):
plt.subplot(1, 5, i+1)
plt.imshow(X_train[i].reshape(28,28), cmap="gray")
plt.title(f"Label: {y_train[i]}")
plt.axis("off")
plt.show()
Quant à l'instruction plt.imshow(X_train[i].reshape(28,28), cmap="gray"), elle affiche l’image correspondante du dataset MNIST en la remodelant au format 28×28 pixels et en la représentant en niveaux de gris pour une meilleure lisibilité.
Le bloc de code précédent produit ce résultat:
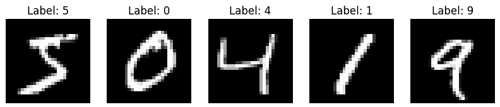
Il est temps de construire notre architecture de CNN:
model = models.Sequential([
layers.Conv2D(32, (3,3), activation='relu', input_shape=(28,28,1)),
layers.MaxPooling2D((2,2)),
layers.Conv2D(64, (3,3), activation='relu'),
layers.MaxPooling2D((2,2)),
layers.Flatten(),
layers.Dense(64, activation='relu'),
layers.Dense(10, activation='softmax')
])
layers.Conv2D(32, (3,3), activation='relu', input_shape=(28,28,1)),
layers.MaxPooling2D((2,2)),
layers.Conv2D(64, (3,3), activation='relu'),
layers.MaxPooling2D((2,2)),
layers.Flatten(),
layers.Dense(64, activation='relu'),
layers.Dense(10, activation='softmax')
])
La premire couche Conv2D(32, (3,3), activation='relu', input_shape=(28,28,1)) applique 32 filtres (ou kernels) de taille 3x3 sur l’image d’entrée de dimension 28x28x1. Chaque filtre glisse sur l’image (convolution) et extrait des motifs locaux comme des bords ou des textures. Le résultat est un ensemble de cartes de caractéristiques (feature maps) qui traduisent la présence de ces motifs dans différentes zones de l’image. L’activation ReLU est ensuite appliquée pour introduire de la non-linéarité et éviter que le modèle ne se limite à des combinaisons linéaires des pixels.
Dans le code précédent, nous avons directement précisé la forme d’entrée (input_shape) dans la première couche convolutionnelle, mais il aurait aussi été possible d’utiliser une couche Input séparée pour définir explicitement la taille des données en entrée (comme on l'a vu dans les leçons précédentes).
La deuxième couche MaxPooling2D((2,2)) réalise une opération de pooling qui consiste à réduire la taille des cartes de caractéristiques produites par les filtres de convolution. Concrètement, elle parcourt l’image avec une fenêtre de 2x2 et conserve uniquement la valeur maximale de chaque bloc, ce qui permet de diminuer la dimension spatiale (par exemple de 28x28 à 14x14) tout en gardant les informations les plus représentatives. Cette étape rend le modèle plus efficace en réduisant le nombre de paramètres et en limitant le risque de surapprentissage tout en mettant en avant les motifs les plus saillants détectés par les kernels.
On peut répéter plusieurs fois l’enchaînement Conv2D et MaxPooling2D, en ajustant à chaque étape les hyperparamètres comme le nombre de filtres, la taille du kernel (par exemple 3x3 ou 5x5) ou encore le type de pooling (max pooling, average pooling), afin de construire une hiérarchie de représentations visuelles de plus en plus abstraites et adaptées au problème de classification.
La couche Flatten() sert à transformer les cartes de caractéristiques multidimensionnelles issues des convolutions et du pooling en un vecteur unidimensionnel afin de les rendre compatibles avec les couches entièrement connectées (Dense) qui attendent des entrées sous forme de vecteurs.
La couche Dense(64, activation='relu') est une couche entièrement connectée qui prend le vecteur aplati en entrée et applique 64 neurones pour combiner les caractéristiques extraites, tandis que la couche Dense(10, activation='softmax') constitue la sortie du réseau avec 10 neurones correspondant aux classes possibles et utilise la fonction softmax pour transformer les scores en probabilités de classification.
L'étape suivante consiste à compiler notre modèle:
model.compile(
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy']
)
Ensuite on lance son entrainement:
optimizer='adam',
loss='categorical_crossentropy',
metrics=['accuracy']
)
model.fit(
X_train,
y_train_cat,
epochs=5,
batch_size=64,
validation_split=0.1
)
Puis, on l'évalue:
X_train,
y_train_cat,
epochs=5,
batch_size=64,
validation_split=0.1
)
test_loss, test_acc = model.evaluate(X_test, y_test_cat)
print("Exactitude sur le jeu de test: ", test_acc)
La méthode model.evaluate() retourne la valeur de la fonction de perte calculée sur le jeu de données fourni, ainsi que toutes les métriques définies lors de la compilation du modèle.
print("Exactitude sur le jeu de test: ", test_acc)
On obtient ce résultat:
313/313 ━━━━━ 3s 10ms/step - accuracy: 0.9899 - loss: 0.0289
Exactitude sur le jeu de test: 0.9898999929428101
Le résultat indique que le modèle a évalué 313 lots (batches) du jeu de test en 3 secondes environ, avec un temps moyen de 10 ms par lot. Les résultats montrent une exéctitude (accuracy) de 98,99 % et une perte (loss) de 0,0289, ce qui signifie que le modèle classe correctement presque toutes les images du jeu de test.
Exactitude sur le jeu de test: 0.9898999929428101
Pour finir, on procède à quelques prédictions:
plt.figure(figsize=(10, 2))
for i in range(5):
plt.subplot(1, 5, i+1)
plt.imshow(X_test[i].reshape(28,28), cmap="gray")
prediction = model.predict(X_test[i].reshape(1,28,28,1))
predicted_label = np.argmax(prediction)
plt.title(f"Prédit: {predicted_label}nRéel: {y_test[i]}")
plt.axis("off")
plt.show()
Ce code affiche 5 images du jeu de test et le modèle prédit la classe pour chacune d'entre elles. L’image est représentée en niveaux de gris, puis la prédiction est obtenue en prenant l’indice du score maximal avec np.argmax (comme on l'a vu dans la leçon consacrée à la classification multiclasses).
for i in range(5):
plt.subplot(1, 5, i+1)
plt.imshow(X_test[i].reshape(28,28), cmap="gray")
prediction = model.predict(X_test[i].reshape(1,28,28,1))
predicted_label = np.argmax(prediction)
plt.title(f"Prédit: {predicted_label}nRéel: {y_test[i]}")
plt.axis("off")
plt.show()
L'exécution du code précédent produit ce résultat:
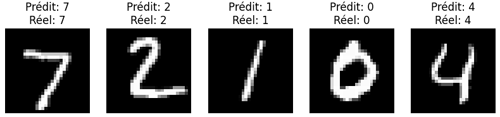
Je n’ai pas détaillé toutes les portion du code, car plusieurs éléments (comme les couches convolutionnelles, le pooling, la compilation ou l’évaluation) ont déjà été expliqués auparavant. Ici, l’objectif est surtout de montrer la logique globale et l’application pratique du modèle sans répéter les explications déjà traitées en détail.
Leçon 13
CNN et MNIST: reconnaissance et classification des chiffres manuscrits
CNN et MNIST: reconnaissance et classification des chiffres manuscrits


