Classification binaire pour la prédiction de survie au bord du Titanic

Prédiction de survie au bord du Titanic à l'aide d'un réseau de neurones

Dans le cadre de cet exemple, nous allons procéder à la prédiction de la survie des passagers du Titanic en formulant le problème comme une classification binaire.

Chaque individu est associé à une étiquette (1 s’il a survécu, 0 sinon). Pour ce faire, nous mobiliserons un réseau de neurones artificiels construit avec Keras/TensorFlow. Ce modèle, composé de plusieurs couches denses et activations non linéaires, sera entraîné sur les caractéristiques disponibles (âge, sexe, classe, etc.) afin d’apprendre à distinguer les profils de passagers susceptibles de survivre.

L’utilisation d’une couche de sortie sigmoïde permettra de générer une probabilité de survie comprise entre 0 et 1, que nous transformerons ensuite en prédiction binaire.

Architecture complète du réseau de neurones appliqué à la classification binaire

Encore une fois, je vais vous montrer le code complet en une seule fois, puis je m'arrêterai sur les partie qu inécessitent des exiplications détaillées.
Comme pour chaque projet, on commence par importer les modules nécessaires. Cette fois, nous allons faire les choses proprement et nous procéderons à la séparation des données de l'entrainement des données de test à l'aide du module train_test_split.

Vous avez certainement remarqué l'importation des métriques precision et recall:
Dans Keras, il n’est pas recommandé d’indiquer directement "precision" et "recall" comme chaînes de caractères dans la fonction compile car ces noms ne correspondent pas à des métriques intégrées par défaut. En effet, Keras ne reconnaît que certaines métriques standards (comme "accuracy"), tandis que la précision et le rappel doivent être importés explicitement sous forme de classes (Precision() et Recall()) depuis tensorflow.keras.metrics.

Concernant la construction du modèle, il y a un tout petit changement par rapport à l'exemple de la leçon précédente:
En effet, nous avons utilisé la fonction d'activation sigmoid pour la couche de sortie afin d'implémenter une classification binaire (sous forme de probabilité comprise entre 0 et 1). Lors de la dernire leçon, nous n'avons appliqué aucune fonction d'activation à cette couchce car il il s'agissait d'un problème de régression.

Dans la couche d'entrée, au lieux d'expliciter directement le nombre de feature 6, nous l'avons renseigné dynamiquement à l'aide de X.shape[1].

L'étape suivante consiste à configurer le réseau de neurones pour une classification binaire:
La fonction de perte binary_crossentropy mesure l’écart entre les probabilités prédites et les vraies étiquettes (0 ou 1), l’optimiseur adam ajuste efficacement les poids du modèle. Quant aux métriques accuracy, Precision() et Recall(), elles permettent de suivre respectivement la proportion de prédictions correctes, la précision des prédictions positives et la capacité du modèle à détecter les vrais positifs.

Dans cet exemple, nous avons procédé à la séparation les données d'entrainement et du test conformément aux bonnes pratiques en data science:
Vient ensuite la phase d'entrainement de notre modèle:
Le modèle est entraîné sur les données X_train et y_train pendant 200 époques. L’argument validation_split=0.2 indique que 20% des données d’entraînement seront automatiquement réservées pour l’évaluation interne du modèle à chaque époque. La variable history stocke ensuite toutes les informations de l’entraînement (valeurs de la loss et des métriques par époque), ce qui permet de tracer les courbes d’apprentissage et d’analyser la progression du modèle.

Voilà un extrait du rapport d'entrainement concernant la première époque:
Une étape essentielle consiste à transformer les probabilités produites par le modèle en prédictions binaires exploitables:
La commande model.predict(X_test) génère pour chaque exemple du jeu de test une probabilité de survie (issue de la fonction sigmoïde). Ensuite, l’expression (y_pred_proba > 0.5).astype("int32") applique un seuil de décision, autement dit, si la probabilité est supérieure à 0.5, l’étiquette est fixée à 1 (survie), sinon à 0 (non‑survie).

L’utilité de cette étape est donc de convertir les sorties continues du réseau en classes discrètes, ce qui permet d’évaluer le modèle avec des métriques de classification comme l’accuracy, la précision ou le rappel.

La suite des instructions représente la phase classique de tout projet de classification comprenant l’évaluation du modèle, la génération d’un rapport de classification et la production de supports visuels complémentaires tels que la matrice de confusion.

A titre d'exemple, voilà à quoi ressemble la matrice de confusion dans notre cas:
Visualisons la courbe d’apprentissage (Learning Curve) de notre modèle:
L'exécution de ces instrcutions produit ce graphique:

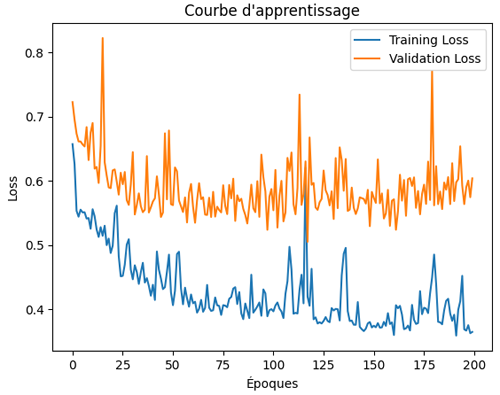
La courbe d’apprentissage montre que le modèle apprend bien sur les données d’entraînement puisque la loss générale diminue malgré les oscillations (zigzag liés au bruit ou à la taille des batchs). En revanche, la val_loss baisse au début, ce qui indique une bonne généralisation initiale, puis elle se stabilise et remonte légèrement vers la fin. Ce comportement traduit un début d’overfitting: le réseau continue à s’améliorer sur l’entraînement mais perd en capacité de généralisation sur les données de validation.