Régression linéaire: mise en œuvre avec Keras

Apprendre une relation simple avec un réseau de neurones

Dans ce cas d’étude, nous allons générer un jeu de données artificiel pour illustrer l’utilisation de Keras dans un problème de régression. L’idée est de créer une variable explicative X à une dimension (feature) et une variable cible y (target) qui dépend de X selon une relation linéaire simple. Pour rendre l’expérience plus réaliste, on injecte un petit bruit aléatoire dans y, ce qui simule les imperfections et la variabilité que l’on retrouve dans des données réelles.

L’objectif est de construire un réseau de neurones avec Keras capable d’apprendre cette relation entre X et y. Concrètement, nous voulons :

1. Définir un modèle séquentiel simple (quelques couches denses).
2. Spécifier une fonction de coût adaptée à la régression (par exemple l’erreur quadratique moyenne, MSE).
3. Utiliser un optimiseur moderne (Adam) pour améliorer la convergence.
4. Entraîner le modèle sur nos données artificielles et observer comment il parvient à approximer la relation sous-jacente malgré le bruit.

Construire le réseau de neurones pas à pas

On commence par importer les bibliothèques nécessaires pour construire et entraîner un petit réseau de neurones.
Dans ce code, NumPy (que nous avons déjà eu l'occasion d'utiliser dans le cours de Machine Learning) est utilisé pour générer et manipuler des données numériques qui serviront de feature X et de target y.

La librairie Keras, via les modules Sequential, Input et Dense, permet de définir le modèle de régression à base de réseau de neurones:

• Sequential: Le modèle Sequential (que l'on importe depuis tensorflow.keras.models) est une structure qui permet d’empiler les couches du réseau les unes après les autres. Chaque couche prend en entrée la sortie de la précédente, ce qui rend la construction du modèle intuitive et claire (comme on le verra dans la suite du code).
• Input: La couche Input définit la forme des données qui entrent dans le réseau. Cette étape est essentielle car elle informe le modèle sur la taille et la structure des données qu’il doit traiter dès le départ.
• Dense: La couche Dense est une couche entièrement connectée où chaque neurone est relié à tous ceux de la couche précédente. Elle permet d’apprendre la relation entre les variables d’entrée X et la cible y. En ajustant les poids et les biais, elle construit progressivement une fonction d’approximation capable de modéliser la relation.

Matplotlib est importé pour visualiser les données et les résultats de l’entraînement, tandis que la fonction randint du module random permet d’injecter un bruit aléatoire dans les données afin de simuler des conditions réalistes.

La prochaine étape consiste à générer les valeurs de la feature X et le target y:
La variable X est construite comme un tableau NumPy contenant les entiers de 0 à 99, puis transformée en une matrice colonne grâce à reshape(-1,1) afin de représenter une feature unidimensionnelle. La variable y est définie comme une relation linéaire simple (y=2X), mais avec un bruit aléatoire injecté via randint(-10,10) pour chaque valeur. Ce bruit simule les imperfections des données réelles et rend l’apprentissage plus réaliste.

Ainsi, on obtient un dataset où la cible y dépend de X de manière approximativement linéaire, ce qui constitue une base idéale pour entraîner un modèle de régression avec Keras et observer comment il parvient à retrouver la tendance malgré la variabilité.

Maintenant, il est temps de constuire notre réseau couche par couce à l'aide de Keras:
Ce bloc de code définit la structure du réseau de neurones avec Keras. On commence par créer un modèle Sequential qui permet d’empiler les couches de manière linéaire:

1. La première couche est un Input avec une dimension de 1 (qu'on a spécifiée à l'aide du tuple (1,)), ce qui correspond à notre feature X.
2. Ensuite, on ajoute une couche Dense de 50 neurones avec l’activation ReLU, ce qui permet au modèle de capturer des relations non linéaires et de mieux gérer la variabilité introduite par le bruit dans les données.
3. Enfin, une dernière couche Dense avec un seul neurone est ajoutée pour produire la sortie y adaptée à une tâche de régression. Dans ce cas aucune fonction d'activation n'est définie pour conserver la sortie brute du neurone.

La méthode add() en Keras est utilisée pour ajouter une nouvelle couche au modèle lorsqu’on construit un réseau de neurones avec l’API Sequential. Chaque appel à add() insère une couche supplémentaire dans la pile en respectant l’ordre séquentiel. Par conséquent, la sortie de la couche précédente devient l’entrée de la suivante.

Il existe une alternative à la méthode add() pour définir un modèle Keras.
Ici, toutes les couches sont directement passées dans le constructeur de Sequential([...]) sous forme de liste.

L'étape suivante consiste à préparer le modèle pour l’entraînement (compilation du modèle):
La compilation du modèle se faitn en définissant trois éléments essentiels:

• loss="mse": La fonction coût (loss function). Nous avons choisi est la Mean Squared Error (erreur quadratique moyenne) adaptée aux problèmes de régression car elle mesure l’écart entre les prédictions du modèle et les valeurs réelles.
• optimizer="adam": L’optimiseur utilisé est Adam qui combine les avantages du momentum et de RMSProp pour assurer une convergence rapide et stable.
• metrics=["mse","mae"]: En plus de la fonction de coût, on demande au modèle de suivre deux métriques pendant l’entraînement: la MSE et la MAE (Mean Absolute Error), ce qui permet d’évaluer la performance du modèle sous différents angle.

On peut obtenir une vue d’ensemble de l’architecture du réseau de neurones construit à l'aide de cette instruction:
Ce qui donne:

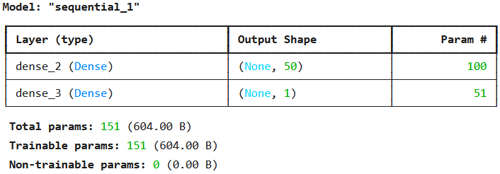
Le résumé affiché par model.summary() montre la structure interne du réseau. La première ligne correspond à une couche Dense de 50 neurones recevant une entrée de dimension 1. L’Output Shape (None, 50) signifie que pour chaque échantillon en entrée, la sortie est un vecteur de 50 valeurs, et le None indique que la taille du batch est flexible (il sera renseigné lors de l'entrainement). Le nombre de paramètres est 100, ce qui correspond aux 50 poids (un par neurone pour la feature d’entrée) plus 50 biais.

La seconde ligne décrit la couche Dense de sortie avec un seul neurone: son Output Shape est (None, 1) et elle possède 51 paramètres, soit 50 poids (un par connexion avec chaque neurone de la couche précédente) plus 1 biais.

Ce résumé permet de vérifier la cohérence du modèle et de comprendre comment les paramètres sont distribués entre les couches.
Il est temps d'entrainer notre modèle:
La méthode fit (qui nous est familière) prend en entrée les données X (features) et y (cibles) et ajuste les poids du réseau pour réduire l’erreur définie par la fonction de coût (MSE dans ton cas).

L’argument epochs=50 indique que l’ensemble des données sera parcouru 50 fois, ce qui permet au modèle de mieux apprendre la relation entre X et y.

À chaque époque, l’optimiseur (Adam) met à jour les paramètres du réseau en fonction des gradients calculés.
Par défaut, la taille du lot (batch size) traité à chaque itération est de 32. Toutefois, il est possible de modifier cette valeur en la précisant explicitement dans l’instruction d’entraînement, par exemple:
L’évolution de l’entraînement est illustrée par cette illustration où l’on observe la diminution progressive de l’erreur au fil des époques.

Le message affiché pendant l’entraînement correspond au suivi des époques. Par exemple, lors de la première époque, 4/4 indique que l’ensemble des données a été divisé en 4 batches et que le modèle vient de terminer le dernier lot de cette époque. Le temps d’exécution est précisé (3s au total, 44ms par batch). Ensuite, les métriques sont affichées.

On évalue notre modèle:
Ce qui produit ce résultat:
Lors de l’évaluation, la sortie affichée indique que le modèle a traité les 4 batches de données en 0 seconde au total, avec environ 15 ms par batch.

Les métriques montrent une loss et une MSE de 452.33 (identiques puisque la fonction de coût choisie est la MSE), ainsi qu’une MAE de 17.59, ce qui signifie que l’écart moyen entre les prédictions et les valeurs réelles est d’environ 18 unités.

Le tableau final [452.3371, 452.3371, 17.5966] reprend ces résultats sous forme numérique: première valeur = loss, deuxième = MSE et troisième = MAE. Cela permet de juger objectivement la performance du modèle après l’entraînement.
On peut désormais tracer la droite de régression (valeur prédites) et la positionner par rapport au nuage de points réels.
Ce qui produit ce graphique:

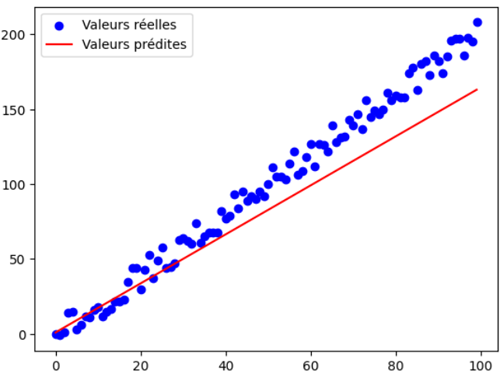
La droite de régression obtenue apparaît légèrement décalée par rapport aux valeurs réelles, ce qui s’explique par le nombre d’époques relativement limité (50) utilisé lors de l’entraînement.

En effet, un réseau de neurones a généralement besoin d’un nombre plus élevé d’époques et d’un volume conséquent de données pour affiner ses paramètres et parvenir à une meilleure généralisation. Ce décalage illustre donc la nature progressive de l’apprentissage: plus le modèle est exposé aux données sur de longues itérations, plus il est capable de rapprocher ses prédictions de la réalité.

Augmentons le nombre d'éppoques à 100 par exemple:
Cette fois on obtient ce graphique:

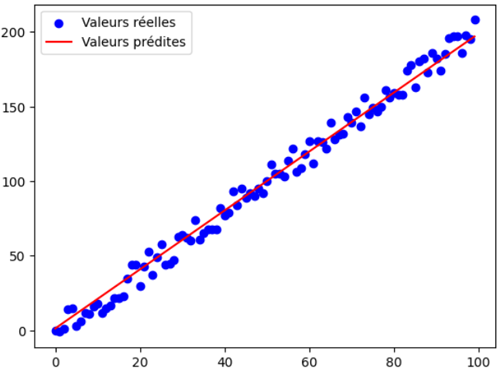
Avec 100 époques, la droite de régression s’ajuste beaucoup mieux au nuage de points et reflète fidèlement la tendance des données.