Mise en pratique de la régularisation avec Keras

Dans cette leçon, nous allons reprendre l’exemple de la dernière fois portant sur la classification binaire et montrer comment appliquer différentes techniques de régularisation pour améliorer la généralisation du modèle.

Afin de rester concis, nous n’allons pas réécrire le code complet, mais uniquement les parties qu’il faut modifier.

Si vous voulez explorer le code complet, je vous inviter à consulter la leçon dédiée à la classification binaire sur le dataset Titanic.

Je rappelle que la courbe d'apprentissage (learning curve) que nous avons obtenue ressemble à ceci:


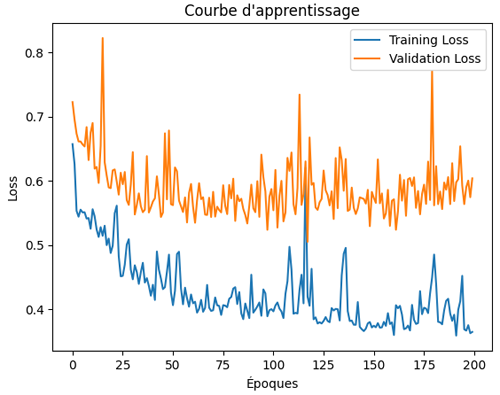
On constate un début d'overfitting entre l'époque 100 et l'époque 150, vu que la validation loss grimpe petit à petit alors que le training loss continue à baisser.

Application de la régularisation L1 (Lasso)

Afin d'appliquer la régularisation L1 (ou régularisation Lasso), on applique les modifications suivantes à notre code:
On commence par importer la fonction de régularisation L1 depuis le module regularizers de Keras. Puis on ajoute l’argument kernel_regularizer=l1(0.01) qui signifie que l’on applique une régularisation L1 sur les poids de ces couches.

Concrètement, cela introduit une pénalité proportionnelle à la somme des valeurs absolues des poids dans la fonction coût, ce qui pousse certains poids à devenir exactement nuls. L’effet attendu est de simplifier le modèle en réduisant le nombre de paramètres effectivement utilisés, ce qui peut améliorer la généralisation et limiter le sur-apprentissage. Le coefficient 0.01 contrôle l’intensité de cette régularisation: plus il est élevé, plus la contrainte est forte.

La learning curve obtenue ressemble à ceci:

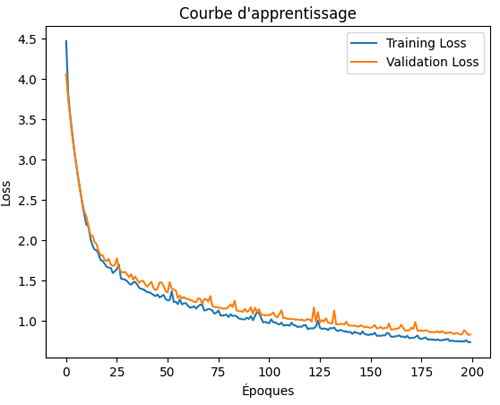
On observe que, cette fois-ci, la validation loss diminue de manière régulière, ce qui indique une bonne capacité de généralisation du modèle et l’absence de signes d’overfitting. Néanmoins, il reste possible d’augmenter le nombre d’époques afin de poursuivre l’amélioration des performances et d’affiner davantage l’apprentissage.

Application de la régularisation L2 (Ridge)

Pour appliquer la régularisation L2 (aussi connue sous le nom de régularisation Ridge ou Weight Decay), on procède exactemement comme pour l'exemple précédent, sauf qu'on remplace L1 par L2:
Cette fois, la learning curve ressemble à ceci:

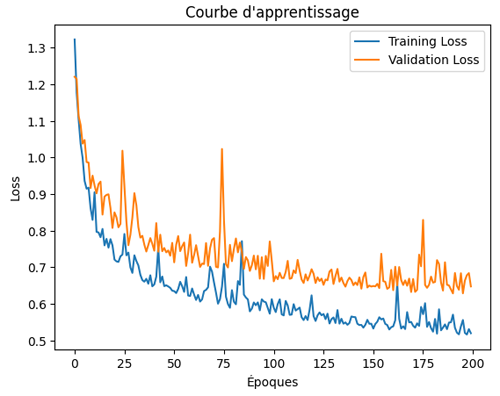
On constate la même tendance générale que celle observée avec la régularisation L1, c'est à dure une validation loss qui continue à baisser, indiquant l'absence d'overfitting.

Application de la régularisation Dropout

Cette fois, le code ressemblera à ceci:
Dans ce code, on commence par importer la classe Dropout depuis tensorflow.keras.layers, ce qui permet d’utiliser cette technique de régularisation dans la définition du modèle. Ensuite, deux couches Dropout(0.5) ont été ajoutées juste après chacune des couches Dense cachées de 50 neurones. Concrètement, cela signifie qu’à chaque étape de l’entraînement, 50% des neurones de la couche précédente sont désactivés de manière aléatoire. Cette stratégie empêche le réseau de trop dépendre de certains neurones spécifiques, réduit le risque de sur-apprentissage (overfitting), et favorise une meilleure généralisation du modèle.

Ainsi, l’importation de Dropout et son insertion après les couches denses constituent les modifications essentielles pour appliquer cette régularisation.

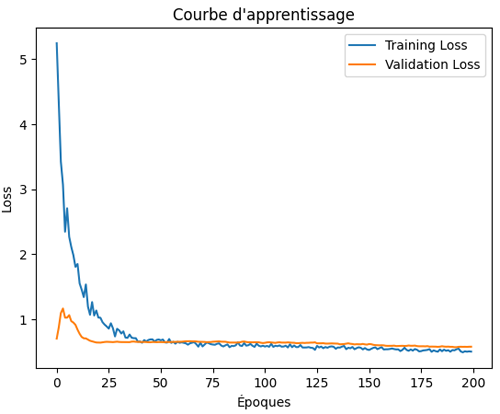
L’effet du Dropout sur cette courbe d’apprentissage se traduit par une diminution régulière et parallèle des pertes d’entraînement et de validation. En désactivant aléatoirement une partie des neurones à chaque époque, le modèle évite de trop mémoriser les données d’entraînement et parvient à mieux généraliser, ce qui explique l’absence de divergence entre les deux courbes et la stabilité observée.

Application de la régularisation Batch Normalization

Le code suivra la même logique que celle qui inclue la régularisation Dropout:
La fonction BatchNormalization() s’utilise très simplement. En effet, il suffit de l’appeler sans préciser de paramètres particuliers. Par défaut, elle normalise automatiquement les activations de la couche précédente en ajustant leur moyenne et leur variance, puis applique des coefficients d’échelle et de décalage appris pendant l’entraînement. Ainsi, on n’a pas besoin de configurer manuellement ses paramètres.

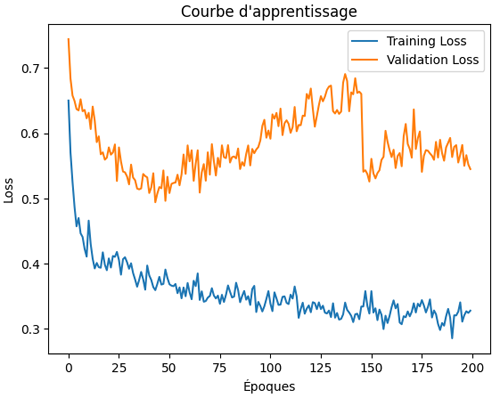
On observe que la loss d’entraînement diminue de façon régulière, ce qui montre que le réseau parvient à apprendre efficacement. En revanche, la loss de validation reste instable et fluctue au fil des époques, sans suivre une tendance clairement descendante. Cela traduit une difficulté du modèle à généraliser correctement sur les données de validation, malgré la stabilisation apportée par la normalisation des activations.

En résumé, la Batch Normalization contribue à rendre l’entraînement plus stable et à accélérer la convergence, mais elle ne garantit pas à elle seule une bonne généralisation. En effet, il est souvent recommandé de l'utiliser avec d'autres techniques comme L1, L2 ou Early Stopping.

Application de la régularisation via Early Stopping

Cette fois, le code sera un peu différent par rapport aux techniques qu'on a vu précédemment:
Comme d'habitude, on importe les modules nécessaires. Cette fois, c'est la classe EarlyStopping à partir de tensorflow.keras.callbacks.

Ensuite, on définit le callback. En effet, un callback dans Keras est un mécanisme qui permet d’exécuter automatiquement certaines actions pendant l’entraînement du modèle sans avoir à les coder manuellement dans la boucle. Dans notre cas, le callback utilisé est EarlyStopping, dont le rôle est d’arrêter l’entraînement lorsque la performance sur les données de validation cesse de s’améliorer.

Les paramètres que l'on a définit dans le callback sont:

• monitor="val_loss": signifie que l’on suit l’évolution de la perte sur les données de validation, ce qui est pertinent car c’est précisément cette métrique qui permet de détecter un éventuel sur-apprentissage (overfitting).
• patience=10: signifie que si la perte de validation ne s’améliore pas pendant 10 époques consécutives, l’entraînement s’arrête automatiquement.
• restore_best_weights=True: permet de restaurer les poids du modèle correspondant à la meilleure performance observée, plutôt que de conserver ceux de la dernière époque.

Dans l’instruction de l'entrainement model.fit(), l’argument callbacks=[early_stop] indique que l’on associe au processus d’entraînement le callback défini précédemment. Autrement dit, à chaque époque, Keras exécute automatiquement les instructions contenues dans early_stop. C'est à dire, il surveille la perte de validation (val_loss), arrête l’entraînement si aucune amélioration n’est observée après 10 époques consécutives (patience=10), et restaure les meilleurs poids atteints (restore_best_weights=True).
Cette fois, le learning curve produite ressemble à ceci:

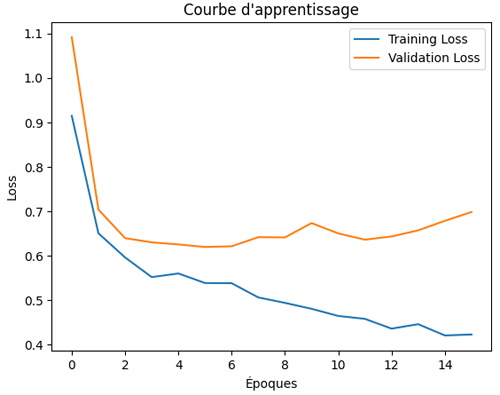
La courbe d’apprentissage montre que l’entraînement s’est interrompu automatiquement à l’époque 15 grâce au mécanisme d’Early Stopping. Cela signifie que la perte de validation n’a plus présenté d’amélioration significative pendant 10 époques consécutives et que le modèle a donc cessé l’entraînement avant d’atteindre les 200 époques prévues.

Cette interruption précoce de l'entrainement évite le sur-apprentissage et garantit que les poids conservés correspondent à la meilleure performance observée sur les données de validation.