Convolutions: le secret derrière la reconnaissance d’images

Pourquoi les CNN? Limites des réseaux fully-connected face aux images

Jusqu’ici, nous avons vu que les réseaux de neurones classiques (fully-connected) peuvent traiter des données tabulaires ou des vecteurs simples, mais ils montrent rapidement leurs limites lorsqu’il s’agit d’images.

Prenons une image relativement petite de 32×32 pixels. Cela représente déjà 1024 pixels au total. Or, chaque pixel en couleur est décrit par trois composantes (rouge, vert, bleu), ce qui fait 3 valeurs par pixel. Ainsi, le vecteur d’entrée correspondant à cette image contient 3072 valeurs numériques (1024 × 3).

Si l’on connecte chaque pixel à chaque neurone, le nombre de paramètres explose, rendant l’apprentissage coûteux et inefficace. De plus, un réseau dense ignore la structure spatiale de l’image. Pour lui, un pixel en haut à gauche n’a aucune relation particulière avec son voisin immédiat, alors que dans la réalité, les motifs visuels (bords, textures, formes) dépendent fortement de la proximité locale.

Prenons un exemple concret: si l’on veut reconnaître un chiffre manuscrit, un réseau dense doit apprendre séparément chaque variation possible de chaque pixel, tandis qu’un CNN peut apprendre un filtre simple qui détecte les contours, puis combiner ces motifs pour reconstruire la forme du chiffre. Autrement dit, les CNN exploitent la nature bidimensionnelle des images et réduisent drastiquement le nombre de paramètres tout en capturant les régularités locales. C’est cette capacité à "voir" et à extraire des caractéristiques visuelles pertinentes qui fait des CNN l’outil incontournable pour le traitement d’images.

Qu'est ce que les Convolutional Neural Networks ou CNN?

Les Convolutional Neural Networks (CNN) sont une famille particulière de réseaux de neurones conçus pour traiter efficacement les données visuelles. Leur principe repose sur l’utilisation de kernels (ou filtres) qui permettent d’extraire automatiquement des motifs caractéristiques dans les images, ainsi que sur des opérations de pooling qui réduisent la dimension tout en conservant l’essentiel de l’information.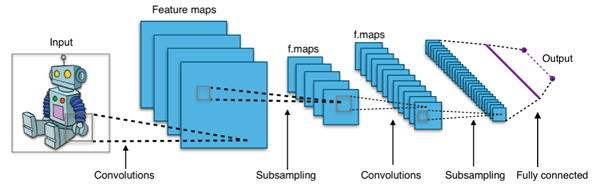

Ces mécanismes, combinés à des couches classiques de neurones, donnent aux CNN la capacité de reconnaître et de hiérarchiser des structures visuelles de plus en plus complexes, ce qui en fait l’architecture de référence pour l’imagerie et la vision par ordinateur.

Convolutional Neural Networks: une architecture polyvalente qui va au delà des images

Bien que les CNN soient principalement connus pour leurs performances exceptionnelles en traitement d’images et en vision par ordinateur, leur utilisation ne se limite pas à ce domaine. Grâce à leur capacité à extraire automatiquement des motifs locaux dans des données structurées, ils sont également appliqués dans d’autres contextes, notamment:

• Analyse de texte (NLP): Dans ce contexte, les mots ou les phrases sont représentés sous forme de vecteurs numériques (embeddings), et les convolutions permettent d’identifier des motifs linguistiques locaux, comme des associations de mots ou des structures syntaxiques.
• Reconnaissance vocale et le traitement du signal audio: Dans ce domaine, le son est généralement transformé en représentations visuelles comme les spectrogrammes qui traduisent l’intensité des fréquences au fil du temps.
• Analyse de séries temporelles: (Où les données évoluent au fil du temps). Dans le domaine de la finance, par exemple, les cours boursiers ou les indicateurs économiques sont des séquences numériques que les CNN peuvent analyser pour détecter des motifs récurrents, comme des tendances haussières ou des anomalies de marché.

Ainsi, les CNN constituent une architecture polyvalente qui dépasse largement le cadre de l’imagerie.

Mode de fonctionnement d'un CNN

Convolution et kernels: le moteur des CNN

La convolution est le cœur du CNN. Elle consiste à appliquer un petit filtre appelé kernel sur différentes régions de l’image afin d’extraire des motifs locaux.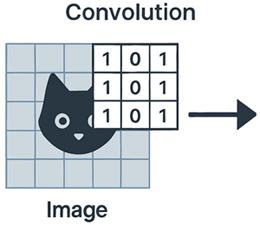

Un kernel est une petite matrice (souvent 3×3, 5×5, etc.) qui glisse sur l’image pour effectuer une opération de convolution. Chaque cellule du kernel contient un poids (valeur numérique) qui sera multiplié par les pixels correspondants de l’image. Le résultat est une combinaison pondérée locale (appliquée aux pixels voisins) qui met en évidence certains motifs comme des bords, des lignes ou des textures.
L’intérêt majeur est que le même filtre est utilisé sur toute l’image, ce qui réduit drastiquement le nombre de paramètres par rapport à un réseau dense et garantit que les motifs appris sont indépendants de leur position.

Les cartes de caractéristiques (feature maps)

Chaque filtre appliqué à l’image génère une feature map, c’est-à-dire une représentation intermédiaire qui met en évidence la présence d’un motif particulier dans différentes zones. Par exemple, une carte peut indiquer où des bords horizontaux apparaissent dans l’image.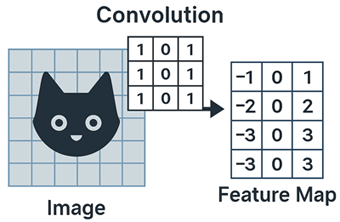

Techniquement, le calcul de la feature map se passe ainsi:

• Fenêtre locale: on place le kernel sur une portion de l’image (par ex. un bloc 3×3 de pixels).
• Multiplication élément par élément: chaque valeur du kernel est multipliée par le pixel correspondant.
• Caldul de la somme: on additionne toutes ces multiplications pour obtenir une seule valeur.
• Placement: cette valeur est placée dans la position correspondante de la feature map.
• Glissement (stride): on déplace le kernel (par ex. de 1 ou 2 pixels) et on recommence.

Si \(I\) est l’image et \(K\) le kernel, la valeur de la feature map en position \((i,j)\) est :

• \(I(i+m,j+n)\) : valeur du pixel de l’image (ou de la feature map précédente) à la position \((i+m,j+n)\).
• \(K(m,n)\) : valeur du filtre (kernel) à la position \((m,n)\).
• \(M\times N\) : taille du kernel (par ex. 3×3).
• \(F(i,j)\) : valeur calculée dans la nouvelle feature map à la position \((i,j)\).

En empilant plusieurs filtres, le CNN construit progressivement une hiérarchie de représentations: les premières couches détectent des motifs simples, tandis que les couches plus profondes combinent ces motifs pour reconnaître des formes complexes comme des yeux, des roues ou des lettres.

La fonction d’activation (ReLU)

Après chaque convolution, on applique généralement une fonction d’activation, le plus souvent la ReLU (Rectified Linear Unit). Elle transforme les valeurs négatives en zéro et conserve les valeurs positives, ce qui introduit de la non-linéarité dans le modèle. Sans cette étape, le CNN ne pourrait pas apprendre des relations complexes.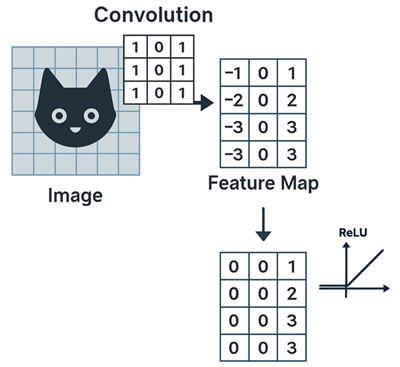

La fonction d'activation ReLU est simple mais efficace car elle accélère l’apprentissage et évite certains problèmes comme la saturation des gradients.

Le pooling

Le pooling est une opération de réduction de dimension qui consiste à résumer une petite région de la feature map par une seule valeur. Le plus courant est le max pooling qui conserve la valeur maximale d’une zone. Techniquement, Le max pooling consiste à faire glisser une matrice (par exemple 2×2) sur la feature map et à ne conserver, dans chaque région parcourue, que la valeur maximale. Cela permet de réduire la taille des représentations, de limiter le nombre de paramètres et de rendre le modèle plus robuste aux petites variations dans l’image (par exemple, un objet légèrement déplacé ou déformé).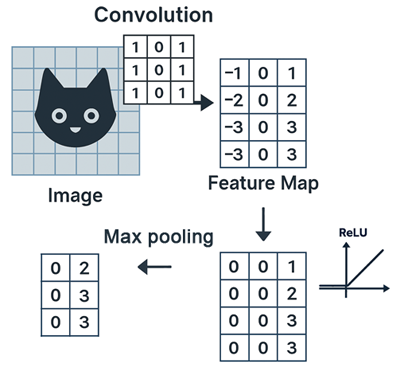

Le pooling agit donc comme une forme de compression intelligente qui conserve l’essentiel de l’information.

Aplatir les feature maps pour les couches fully connected

Après plusieurs étapes de convolution et de pooling, les représentations extraites sous forme de cartes de caractéristiques (feature maps) qui sont des matrices 2D sont aplaties (opération du flattening), c’est-à-dire transformées en un long vecteur 1D. Ce vecteur est ensuite transmis aux couches fully connected, qui jouent le rôle de "décideur" en combinant l’ensemble des caractéristiques détectées pour produire la prédiction finale.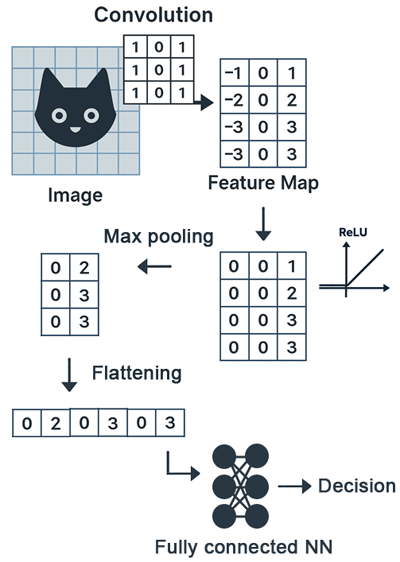

Par exemple, si les couches convolutives ont identifié des yeux, des oreilles et une truffe, la couche fully-connected peut conclure qu’il s’agit d’un chien.

La couche de sortie (Softmax)

Enfin, la dernière couche est généralement une Softmax (dans le cas d’une classification multi-classes). Elle transforme les scores calculés par le réseau en probabilités, indiquant la confiance du modèle pour chaque classe.

Par exemple, le CNN peut prédire qu’une image a 90% de chances d’être un "chat" et 10% d’être un "chien".